Mathematical notes
The purpose of this page is link to documents to inform educators and others on information to facilitate mathematical literacy. Information is organized in four broad areas:
- Mathematical literacy knowledge base of concepts, definitions, outcomes, & outcomes.
- Pedagogical knowledge to develop professionally and create learning experiences to facilitate mathematical literacy and teacher tools to assist.
- Activities, learning units & packets to develop mathematical literacy
- Technology - calculator, programming, and other math related tech
Knowledge base & pedagogical tools for mathematical literacy
Knowledge base
The mathematical knowledge base includes concepts necessary for learners to conceptualize to become mathemtically literate and misconceptions that must be over come. Includes
concepts, outcomes, & vocabulary by content, processes, and attitudinal (values & dispositions) dimensions by levels.
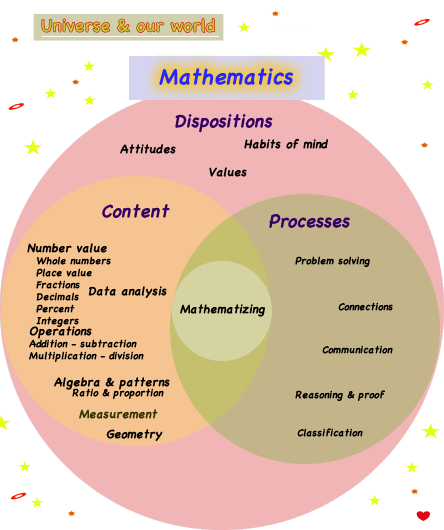
- Algebra & patterns
- Attitudinal (disposition & value statements)
- Classification
- Communication
- Connections & perspectives
- Data Analysis & Probability
- Geometry
- Measurement & measurement estimation
- Number value
- Operations & computation estimation
- Problem solving
- Reasoning & proof
- Relative Position and Motion
- Variable
Information to facilitate mathematical literacy & tools to achieve it
Different fields of mathematics map & explanation video (11:05)
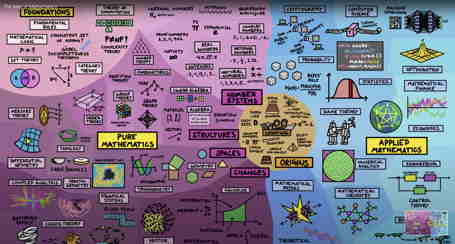
Resources for professional development
- Mathematical vocabulary lists by dimensions & levels
- Definitions of mathematics and focus questions to analyze them
- Kinds of numbers - fact sheet
- Books for professional educators
- Books for professional math educators
- Conceptual and procedural knowledge - Illustrated with card trick magic ...
- Considerations for Planning to Teach: Big ideas, concepts, and generalizations
- General information for professional educators
- Hands on: What is it really?
- History of mathematics in North America
- Independent study: planning guide to help select and refine topics
- Memory: learning basic facts & algorithms - getting learners to slow down & think how to proceed
- Mental math quiz to compare traditional algorithmic solutions to non traditional algorithmic solutions mathematicians are likely to use
- Misunderstood mind on PBS
- Principled procedures for Math Educators
- Reflecting on mathematical instructional practice suggestions
- Sample outline with suggestions for creating a professional portfolio
- Survey your current mathematical practices and research, then compare your thoughts with what current research suggests.
- Mathematical vocabulary lists to review for planning
- Visual & Spatial Representations, Modes of visual learning, Literacy, Research, Activities
Math teacher's planning tool box
General planning
Planning information
- General instructional theory - explanation with examples flexible enough to plan any topic & intended learning
- Overview for planning and creating curriculum documents
- Outline for a year plan and suggestions
- Outline for a sequence or unit plan with suggestions
Examples to prep intended learnings
- Framework with explanations of mapping categories for planning to teach big ideas, concepts or generalizations
- Blank planning map
- Classification sample planning map
- Equality and equal arm balance
- Geometry, Area sample planning map
- Proof and reasoning sample planning map
- Thoughts about math games, competitions, and simulations
- Literature to teach math - Includes - uses of literature to facilitate math literacy, ways to mathematize literature, list of literature books with mathematical themes, literature suggestions by math dimensions, sample lessons using literature books
Suggestions for selecting problems and investigations
- Problems by categories
- Selecting problems '--->> > sample problems with different formats , characteristics of a good problem , guiding questions to prepare mathematical investigations, tasks, or powerful problem
Sample parts and pieces of sequence plans
- Sequence plan with activities to build to cardinality. Good start with multiple concepts, sequence of concepts, and very good lists of activities for concepts. Need more integration of mathematical dimensions for practice of mathemtics and scoring guides with levels.
- Sequence plan for measurement, data analysis, and proportion Includes beginning ideas for integration of mathematical dimensions and some for mathematical practices, good for proportion, could use editing for clarity and more depth of procedures.
Activity plans
- Card trick | Includes integration of mathematical dimensions, good for proof, could use some editing for clarity card trick demonstration with different instructional strategies [conceptual & procedural].
- Reading and writing numbers with numeral and words | Good activity for skill building and necessary skill, doesn't include integration of mathematical dimensions,
- Estimating chocolate chip | Has potential, but needs a lot more information for integration of mathematical dimensions and extended activities.
Assorted tools
- Characteristic of mathematically talented & development of talent
- Mathematics & Logic adapted Frayer Model
- Manipulative materials list
- Parent letter for using manipulatives and representation with multiplication & division
- Eight different uses of literature for teaching mathematics
- Annotated list of literature and classroom uses in NCTM Journals
- Mathematical terms and their representations with Cuisenaire Rods
- Investigations with Cuisenaire rods & student work sheets
- Comparison or English - Spanish wording in math. Translations of some mathematical ideas. Notice how some are the similar and others are very different. Demonstrates that direct translation is generally not as simple as one thinks unless one is bilingual.
- Math Their Way notes
Assessment
- Assessment introduction and review: [Suggestion for creating criteria referenced assessments] [Norm-referenced test information]
- Letter to parents for student lead conferences and authentic assessment
- Questions from standardized achievement tests. SAT, FAA, MCAT, ...
- PISA 2012 Problem-Solving sample questions
- Curriculm Documents with concepts, outcomes, and assessment levels
Sample assessments
- Student survey - open ended about student's math practice - one page
- Student survey - rating sheet (always, mostly, some, not) - about two page
Curriculum
- Comparison of dimensions and categories of NCTM and CCSS of math
- Concepts, suggested sequences, plans, rubrics, and other stuff may be found linked at the top of the page in mathematics content.
- Standards
- Curriculm Documents with concepts, outcomes, and assessment levels
- Rubrics click the desired mathematics dimensions at the top of the page to locate concepts... assessment... evaluation ...
- Notes on exemplary and promising math programs
Workshops, courses, tutorials
- ESU #1 Algebra Workshop information
- Information for graduate Class or professional development
- Information for preservice Class or professional development
- Videos for professional development
- Technology Help Pages - ILife and Windows Media tutorials and help pages for using/ making: photos, audio, and video --->>> directions and tutorials...
- NATM fall conference presentation 2006
- NATM spring conference presentation 2005
- NCTM regional presentation fall 2004
Activities, plans, units, packets, & more to facilitate literacy.
Process dimensions
Content dimensions
Technology, computer programming, software, 3D printing
--- Coding software ---
Mozilla free
Google free
- Made with code - projects, mentors, resources ...
Technology
- History of the cell phone Read... Cell phone mathematics. The story of how Brad Parkinson used creativity and mathematics to enable the use of cell phones.
Math software
- History of graphing software Read: The Graphing Calculator Story by Ron Avitzur, then below the article are links to download the software.
Coding resources
- Spies in the Computer - basic software program and class activity on a 10 x 10 grid
Pedagogical resources
- Viewpoint: Arguments for a LOGO - Pascal Computer Curriculum
- Logo dissertation review by Barbara Elias - Dealing with Logo and the transfer of knowledge from learning one programming program to learning another
3 D printing
*********************
Page Overview
- Mathematical literacy knowledge base of concepts & outcomes
- Learning units, packets, and activities to develop mathematical literacy
- Knowledge to develop professionally and create learning experiences to facilitate mathematical literacy and teacher tools to assist.
- Technology - calculator, programming, & other math related tech ideas
*********************
Other math knowledge base & activity pages
Process dimensions:
Content: dimensions
*********************
*********************
There are 10 kinds of people in the world. Those who understand binary and those who don't.
*********************
Jeffery Weld asks:
Why is it whenever students don't do well on a national test the news agencies report one or a few particular items that were on the test by stating the test questions, then they believe it is necessary to provide the answers.
*********************
If their listeners need the answers, why should we expect students to be able to answer it correctly?
*********************
The Jibaro Indians of the Amazon rain forest express the number five by the phrase:
"wehe amukei,"
"I have finished one hand,"
and the number ten by
"mai wehe amukei,"
"I have finished both hands."
*********************
"These landmarks must not be treated as objectives to be marked off. The goal is to mathematize not pass landmarks. Enjoy the journey create systems to do mathematics with the knowledge that students have. One should recognize the fallacy of thinking there can be one activity or sequence of activities for all students."
*********************
One of the universal customs that man has successfully established on earth is the
Hindu - Arabic numerals
to record numbers.
*********************
Math is meditation for thinking about the world.
Geometry is the science of correct reasoning on incorrect figures.
*********************
Galileo was put under house arrest and allowed visitors, but no mathematicians.
*********************
*********************
Directory links:
*********************
Mathmaticians think about more than math.
Earth will run out of the basic resources, and we cannot predict what will happen after that. We will run out of water, air, soil, rare metals, not to mention oil. Everything will essentially come to an end within fifty years. What will happen after that? I am scared. It may be okay if we find solutions, but if we don’t then everything may come to an end very quickly. Mathematics may help to solve the problem, but if we are not successful, there will not be any mathematics left, I am afraid!
*********************
U.S. Students
Score in the top tier on
the PISA 2012 Math Creative Problem SolvingAssessment
*********************
*********************
*********************