Counting: skip & coral counting
Skip counting by two song!
Youtu.be
Introduction
Skip counting or choral counting can be a problem strategy and a device to develop fluency when used as a review, or warm-up activity, within a lesson, or as closure.
Can vary how count by
- Counting forward and backward.
- Using different kinds of numbers: whole numbers (1, 2, 3, 4, 5, 6, ...), base ten (1, 10, 100, 1000, 10,000, 100,000, 1,000,000, ...) fractions, including improper and mixed numbers, decimals, percentages, integers, and angle measurements.
- Changing the starting point from zero. For example: count by fives and start with six (6, 11, 16, 21, ...)
Procedural considerations
- Decide what numbers to start with and what numbers to count by so learners will be successful. Probably while numbers. Even with experienced learners as success can motivate them to want to be more fluent in knowing the sequence of different numbers.
- Use a freehand, a table, or grid to visualize patterns.
- Explore ways of writing sequences vertically and horizontally with different numbers in the rows and columns to discover which ways illustrate patterns better.
- Anticipate what learners will discover and the order in which they might make those discoveries to be better prepared to guide them to a personalized richer understanding.
- Think about how to start, maybe pair share for a minute to tune up before the a class choral counting.
- Decide what to do if there is a pause in the counting. Start over, back up one or two and start over, ...
- Decide how and when to start recording the sequence so all can see it, how to record, who will write, and how much to record before starting to discuss.
- Start the discussion with: What do you notice?
- Listen, use a lot of silence and wait-time.
- Be surprised by each learner's own unique discoveries.
- Focus on one idea at a time and have learners explain their pattern using the visual so all can see and have them answer ...
- Why does it work? What gives you confidence in knowing it works?
- Encourage others to add their own ways to support other learners explanations with additional explanations.
- When you have additional ideas, try to base them on what learners have previously included. Like ... Look here. What happens if ...
Assessment considerations
- Are all learners positioned so they can view what is being recorded?
- Who is counting and who isn't?
- Are all learners equally attentive to what their classmates are sharing?
- Who is offering constructive ideas?
- Are the learners making connections to the different dimensions of mathematics.
- Do they apply what they learned at times other than skip or coral counting sessions?
- Do they connect the numbers used in the different ways of counting as being related to a universal number system?
- Do they connect different kinds of numbers to equivalent numbers of different types? Fractions - decimals; proper fractions to improper fractions.
- See example for three-fifths.
Challenge:
Count by 2s and explore patterns in the sequence. ![]()
Hint:
- Count by 2s.
- Make a list of groups of twos.
- What do you notice about the numbers?
- Organize them into rows and columns.
- What patterns do you notice?
Discussion:
Count orally: zero, two, four, six, eight, ten, twelve, fourteen, sixteen, eighteen, twenty, ...
Write the digits:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 26, 28, 30, ...
Record the group and number of twos in each group ...
| Number of groups | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total |
Patterns for the digits ...
What about group 100?
Group ...
What patterns can you find when you arrange them in a grid starting a new row when the digits repeat?
Like sample relationships below.
Sample to coral skip count and add notes
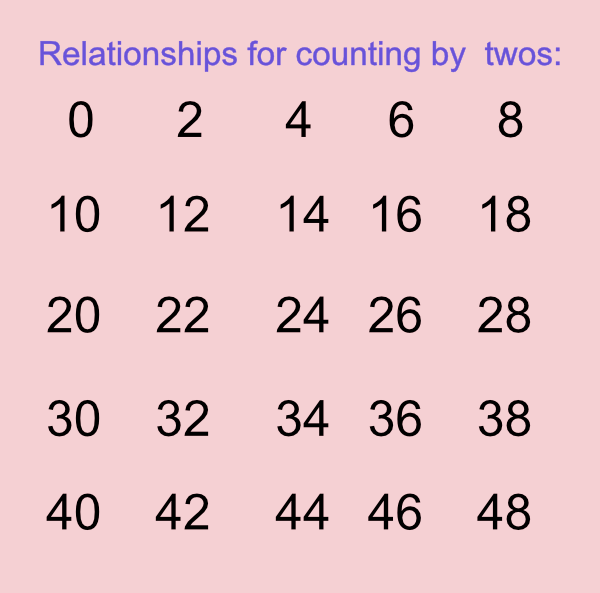
Some patterns:
- Numbers are all even.
- Numbers are 0, 2, 4, 6, 8, then repeat.
- Numbers are multiples of two.
- You add 2 each time.
- Numbers repeat in each group of ten.
- You add 12 diagonally.
- You add 8 diagonally.
- Sample relationships below.
Sample with relationships
Learners can enter relationships for pairs of numbers.
For example ...

As they do they will discover the notation can get fairly compicated quickly. One way to solve the problem would be to use multiple diagrams and decide how to limit the relationships for each. For example all +2 on one sheet and all +10 on another...
Graph
What will a graph look like for the relationship for groups and number of twos?
What will be the difference if the number of groups are graphed as x-values and totals as y-values vs. the number of groups as y-values and totals as x-values.
