Cognitive Development of Reasoning with Supporting Tasks, Activities, & Explanations
- Introduction
- Conservation operations
- General procedure for the tasks and activities
-
Spatial Perception & position
- Position
- Inside, outside, above, below
- Polka-dot in-side, on, out-side of shape
- Reproduction of simple shapes
- Relative position Left & right Egocentric Vs. Allocentric
- Conservation of order with 180 degree rotation
- Rotation of Water in a closed container 45, 90, & 180 degree
- Rotation and Motion 180 degree rotation
- Point of view relative position
- Relative velocity
-
Classification
- Same and different, match, and discriminate
- Class inclusion Subsets of sets
- Class inclusion 2 properties simultaneously
- Seriation order 10 strips
- Simultaneous relationships brothers & sisters
- Class inclusion animals
-
Conservation
- Equivalence or permanence of a set
- One-to-one Correspondence, & conservation of equivalence
- Conservation of number position
- Conservation of number size
- Conservation of length (straw, string, straws)
- Conservation of substance, solid clay
- Conservation of liquid
- Conservation of volume as a liquid
- Conservation area
- Conservation of volume as a solid clay
- Conservation of mass
We’re blind to our blindness. We have very little ideas of how little we know. We’re not designed to know how little we know. Daniel Kahneman
Introduction
This page includes tasks and activities to better understand intellectual development with practical examples of how different levels of development might solve different tasks.
Each task includes several examples of different ways of thinking, which can be used to facilite learning and development with developmentally appropriate teaching and instructional practices. Examples s\that upport the information the development: infant to adult and are necessary for the development of:
These tasks can be used to assess the development of spatial reasoning, conservation and other logical reasoning skills and abilities. They include sample scripts, outcomes with summary, comments, and suggestions. Categories and specific tasks or activities are listed in the overview at the right and all necessary worksheets are linked in the descriptions.
Conservation operations
There are four basic operations necessary for people to be able to conserve and reason. Lack of any one, will cause learners to be mislead and make reasoning errors. They are:
- Egocentric thinking - believe their view is the truth. Inability to differentiate between self and others. Eventually will recognize there are points of view other than their own. What I believe as reality is one way to perceive the world and other people might have a different view. Need to use critical thought, allocentric thought, or sociocentric thought, to differentiate between self and others. Stories and conversations about characters and how their ideas and intentions are different, lead to allocentric thinking.
- Centering - focus on a personal point of view, perception, or sticking with a variable in an illogical way. Need to Decenter. However, to do this, a person must become disequilibrated to begin to consider different information (variables & explanations) with different points of view, which will enable them to reason logically about a situation or problem. Young children are concrete. Seeing is believing. They need to observe and play with materials, properties, data, variables, and ideas in a logical manner to change their beliefs, understandings, and explanations with evidence they experience that contradicts their invalid conclusions.
- Transformation - how something changes or doesn't change when acted on. Young children generally believe something does not change or that it changes instantaneously, without intermediate steps, for example a falling pencil. Faulty reasoning can result in both situations. Acting as if properties are changing when they are not. Or acting as if properties are not changing when they are. Focus on how properties may or may not change in different ways. Before, after, and during examples, videos, and diagrams can promote reasoned thinking about transformations.
- Reversibility - how something changes from one state to another and can or can not be returned to the original state or how something doesn't change when acted on in different ways. This is developed as children focuses on an action as it is done and undone. By asking, Is there an action that can return objects to the original state or undo a change to where it was before the change was imposed; and experiencing the results or lack of results.
Summary
A person must recognize that egocentric thinking can be misleading and other ways of thinking might provide better information. Decenter from misleading perceptions or ideas, use critical thinking, transformations and reversals to reason better. These ideas can be used to understand what actions are conserved and what actions are not. As well as other actions and operations necessary for learners to explore and to develop reasoning and critical thinking.
General procedure for the tasks and activities
This procedure is to be used for one-on-one interviews to collect and record information for individual learners. However, the tasks or activities can be given to groups of learners.
All tasks are best done with learners manipulating physical objects to be concrete representations. Not viewing pictures or listening to stories (iconic or semi-concrete level). However, older children or adults might explore them at a semi-concrete or iconic level to achieve an initial estimation of their thinking.
The way questions are asked can prompt learners in misleading ways. To reduce this possibility ask questions with possible answers as multiple choices. For example, Does one have more or are they equal? Rather than, which is more? or Are they equal?
To a person who has developed a particular reasoning ability, a clue may seem to make it too easy for an accurate test. However, for learners who have not constructed the logical operations needed to reason logically, they will continue to process information for the task in an illogical manner and ignore an accurate answer as illogical to them.
This is okay, however remember, the ultimate goal is for them to be able to conserve in situations when prompts aren't available. As a knowledgeable person needs to be able to identify what properties are necessary and unnecessary and what operation or action is needed to solve any particular problem and accurately justify their reasoning.
Additionally, after a person gives a correct answer, ask for a reason, and if the reason is reasonable, then make a contradictory statement. For example if the person answers correctly.
- Teacher - Is one group more or less or are they equal?
- Student - Both groups are equal.
- Teacher - Why do you think so?
- Student - Because there were no more added or removed.
- Teacher's Contradictory statement - Okay. If I move this one farther away from the others (move it), then there will be more here (point to the group that had one object moved).
- Student - No, they still have the same amount. That one is only farther away, but it is still part of the group.
Because every person is different, it is essential to be willing to deviate from a script as it seems reasonable to do so at the time.
If records are to be made, be sure to record exactly what the person does. What is recorded should allow another person to review it and make a conclusion. If conclusions are to be written, be sure to label them conclusions. Conclusion. The person was unable to conserve length for this task at this time.
General learner procedure:
- Makes a logical statement
- Justifies the statement
- Resists a contradictory statement
- Later, after the assessment task, on a related task is successful. (Adds triangulation)
The procedure is general and may be altered from assessment to assessment as tasks change, or to meet different needs of different learners, or if you discover alternatives you believe would provide different or interesting information.
At anytime a child becomes frustrated, or you believe there may not be any further benefit to continue, then stop.
Tasks or activities
Spatial perception and position
- Position (Inside, outside, above, below) (4.5 years)
- Polka-dot in-side, on, & out-side a shape.
- Reproduction of shapes (square, triangle, circle, rhombus, circle in a square. (6 years)
Materials
Small box, ball, paper and pencil, crayon, or marker and worksheet with images that can be printed and cut out to show one at a time.
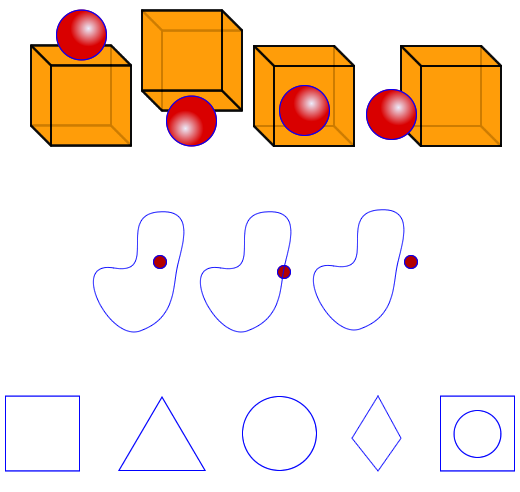
Directions
- Position (Inside, outside, above, below). Show the learner the two objects in each of the three positions one at a time and ask the position of the ball (relative to the box). Ask the learner how they know. If the learner answers correctly and states a plausible reason why, make a contradictory statement.
- Polka-dot in-side, on, & out-side a shape. Show the learner one picture at a time and ask them to draw the shape. Ask them how they know. If they answer correctly and state a plausible reason why, make a contradictory statement.
- Reproduction of shapes (square, triangle, circle, rhombus, circle in a square). Show the learner one picture at a time and ask them to draw each on a piece of paper.
Ask
Position (Inside, outside, above, below).
- Where is the ball?
- Inside, outside, above, below, the box?
- Why?
- If the answers are correct and why is reasonable, make a contradictory statement.
- Repeat for next three positions.
Switch reference point
- Where is the box?
- Inside, outside, above, below, the ball?
- Why?
- If the answers are correct and why is reasonable, make a contradictory statement.
- Repeat for next three positions.
Polka-dot in-side, on, & out-side a shape.
- Where is the polka-dot?
- Inside, outside, or on the line?
- Why?
- If the answers are correct and why is reasonable, make a contradictory statement.
- Repeat for next two positions.
Reproduction of shapes (square, triangle, circle, rhombus, circle in a square).
- Draw the shape.
- Repeat for all five shapes.
- The ball is (inside, outside, above, or below) the box.
- The polka-dot is (on, in, or outside) the shape.
Assessment comments and suggestions
- Locates objects relative to other objects with above, below, inside, and outside.
- Draws a closed figure and marks a position inside, outside, and on the border.
- Identifies simple shapes. Square, circle, triangle, diamond or rhombus, and circle inside square.
- Draws (square, circle, triangle, diamond or rhombus, and circle inside square) as a closed figure, but corners are rounded.
- Draws (square, circle, triangle, diamond or rhombus, and circle inside square) accurately.
Developmental notes
- Learners recognize these simple shapes at three years.
- Learners recognize simple relationships of objects positions relative to each other: above, below, inside, and outside at a fairly young age of about three. It isn't until much later they recognize an object can have two or more relationships simultaneously. Such as the ball is outside and above the box; and the ball is above the box and the box is under the ball.
- Learners draw circles, squares, and triangles first as closed figure adding the necessary properties of the targeted shape more accurately as they age until they are able to recognize properties as sufficient and necessary about age 8.
- Age 6, they will accurately draw acute and obtuse angles of a rhombus or diamond.
Relative Position
Egocentric
Left, Right activity (5 years)
Allocentric left, right activity (7 years)
Materials 
Six different objects (coin, pen, pencil, crayon, marker, sticky note).
Directions
- Ask the learner to hold up their left hand, right hand, point to the assessor's right hand, point to the assessor's left hand. Ask how they know? If accurate make a contradictory statement.
- Set three of the objects (coin, sticky note, pen) in a row from left to right in front of the learner. Ask them the following six questions, ask how they know? and If they are accurate, make a contradictory statement..
- Is the coin to the left or right of the sticky note?
- Is the pen to the left or right of the sticky note?
- Is the coin to the left or right of the pen?
- Is the pen to the left or right of the coin?
- Is the sticky note to the left or right of the coin?
- Is the sticky note to the left or right of the pen?
- Use a different set of objects and arrange them in front of the child in order from left to right. Tell the learner you will let them study them and when they are ready you are going to cover them up with an opaque sheet of paper or folder and ask them the same set off six questions. When they are ready, ask them the six questions. If they are right, ask them how they know they got them right and make a contradictory statement.
Ask
- Hold up your left hand.
- Hold up your right hand.
- Point to my right hand.
- Point to my left hand.
Set of three objects.
- Ask the set of six questions.
- If the answers are correct and their why is reasonable, make a contradictory statement.
Set of six questions:
- Is the coin to the left or right of the sticky note?
- Is the pen to the left or right of the sticky note?
- Is the coin to the left or right of the pen?
- Is the pen to the left or right of the coin?
- Is the sticky note to the left or right of the coin?
- Is the sticky note to the left or right of the pen?
Another set of three objects.
- Use another set of three objects, let memorize, cover, ask set of six questions.
- If the answers are correct and why is reasonable, make a contradictory statement.
- If I were on the other side of the table my right hand would be where your left hand is.
- If you moved to the other side of the table, the coin would still be to the left of the sticky note.
- If the coin were where the pen is it would still be to the left of the sticky note.
Assessment comments and suggestions
- Identified their left and right hand. Miss identified the left and right position of an object relative to another object.
- Identified their left and right hand. Identified the left and right position of an object relative to another object both with the objects visible and hidden.
Developmental notes
- Learners identify their left and right hand with memorization. Some children may have difficulty because of their tendency to reverse positions. Children that know the letter L can use a prompt to assist by making the letter L with their index finger and thumb on their left hand.
- When learners are familiar with their left and right and recognize there are different points of view, they will be able to recognize left and right relative to each person and realize left and right can have two or more points of view simultaneously. Imagine four people sitting in a square each left and right being rotated 90 degrees relative to each person.
Conservation of Order with 180 degree rotation (6 years)
Materials
Three distinct small objects (colored cubes), paper towel tube or wrapping paper tube (opaque). 
Directions
First drop through tube.
- Have the learner order the objects as in a parade.
- Hold your hand on the bottom of the tube so the objects won't leak out.
- Insert the objects into the tube one at a time in the learner's order.
- Ask how they will come out the bottom. What order?
- If the learner answers correctly and states a plausible reason why, make a contradictory statement.
- Can repeat with squares in different positions.
Second drop through tube.
- Have the learner order the objects as in a parade.
- Hold your hand on the bottom of the tube so the objects won't leak out.
- Insert the objects into the tube one at a time in the learner's order.
- Rotate the tube from top to bottom (180 degrees).
- Ask how they will come out the bottom. What order?
- If the learner answers correctly and states a plausible reason why, make a contradictory statement.
- Can repeat with squares in different positions.
Ask
- What will be the order of the objects as they come out of the tube?
- How do you know?
- If the answers are correct and how is reasonable, make a contradictory statement.
- The green (orange, pink) block will be first, then (green, orange, pink), and (green, orange, pink).
Assessment comments and suggestions
- Remembered the order of three objects.
- Conserved the position of three objects as they moved through a tube or tunnel.
- Remembered and conserved the order of three objects. However, did not visually reverse the order when the tube or tunnel was rotated 180 degrees.
- Remembered and conserved the order of three objects and visually reversed the order when the tube or tunnel was rotated 180 degrees.
Developmental notes
Young learners will be amazed by the reversed order and will believe it is a magic trick. If presented as a magic trick to older learners, they will see through the trick, and dismiss it as magic.
Rotation of Water in a closed container 45, 90, 180 degrees (9 years)
Coordinating variables by expanding a system and simultaneously coordinating two variables (jar shape and gravity).
Materials
Two bottles of equal size, one empty, one half full with colored water. One marker or crayon the same color as the colored water. You may consider bottles with or without lids. The picture shows lids. Probably wouldn't need a lid, however, if picture number five didn't have a lid the answer would be different with a puddle of water on the table below the inverted bottle. May want to pose that as task number six. Worksheet with pictures of bottles in the five positions. 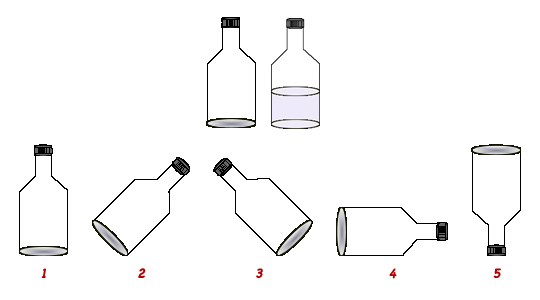
Directions
- Print out the worksheet and cut out the pictures so they can be given to a learner one at a time.
- Start with the bottle half full of colored water. Rotate the bottle into the five different positions:
- upright,
- 45 degrees clockwise,
- 45 degrees counter-clockwise,
- 90 degrees clockwise
- 180 degrees clockwise or counter-clockwise
- After the learner has observed each of the positions, remove the bottle with water from the learner's sight.
- Bring out the empty bottle and place it in the upright position.
- Give the learner one representation of the bottle and ask her or him to draw a line where the water would be in that bottle.
- Ask the learner why they drew the water the way they did.
- If the water level is drawn accurately and the why response is accurate, then make a counter statement.
- Repeat for each image's position.
Ask
- Draw a line where the water would be in this bottle if it were half full of the colored water. (Repeat for each of the five positions.)
- Why did you draw it that way?
- If the answers are correct and why is reasonable, make a contradictory statement.
- Repeat four times.
- I can draw the water this way (trace an incorrect position for the water).
Assessment comments and suggestions
- Draws the water level parallel to the bottom of the jar for each rotations 45, 90, 180 & -45 degrees.
- Draws the water level in the shape of the container with its surface parallel to the Earth. Position determined by Earth's gravity.
Developmental notes
Decenter from previous constructions of water taking the shape of the container and the surface being parallel to the bottom of the container and uses logical reasoning to coordinate the shape of the container and gravities effect on the liquid to draw the water level in the shape of the container so the surface is parallel to the surface of the Earth. Consideration of both variables (shape of the container and the effect of gravity on the surface of a liquid) simultaneously.
180 degree rotation and motion. Going through a rotating tunnel activity (9 years)
Materials
Three distinct small objects (different vehicles or colored cubes), paper towel tube or wrapping paper tube (opaque).
Directions
First time through tunnel.

- Have the learner order the objects as in a parade.
- Insert the objects into the tube and ask how they will come out the other side. What order?
- If the learner answers correctly and states a plausible reason why, make a contradictory statement.
- Can repeat with squares in different positions.
Second time through tunnel.
- Have the learner order the objects as in a parade.
- Insert the objects into the tube.
- Say. While the objects were going through the tunnel there was a great earthquake and the whole mountain and tunnel were spun around 180 degrees. Like this. Turn the tunnel 180 degrees, then ask. What is the order they will come out of the tunnel?
- Can repeat with squares in different positions.
Ask
First time through tunnel
- What will be the order of the objects as they come out of the tunnel?
- How do you know.
- If the answers are correct and why is reasonable, make a contradictory statement.
Second time through tunnel
- What will be the order of the objects as they come out of the tunnel?
- How do you know.
- If the answers are correct and why is reasonable, make a contradictory statement.
- The green block will be first, then ...
Assessment comments and suggestions
- Remembered the order and conserved the positions as the objects moved through the tube or tunnel.
- Remembered the order and visually reversed the order when the tube or tunnel was rotated 180 degrees.
Developmental notes
- Concluded if the objects and vehicles kept moving in the same direction after the earthquake than before, they would come out in the same order they entered and on the same side of the mountain.
Point of view Relative position activity (10 years)
Materials
Three objects to arrange on a table. Four pictures of the arrangement each 90 degrees of the other. Sample: | image 1 | image 2 | image 3 | image 4 |
Directions
- Arrange the objects on the table and have the learner move around the table and sit on each side of the table and observe the objects.
- After moving have the learner sit at one of the four positions and have them select the picture that represents where they are sitting.
- Sit across the table from the learner and ask them to find the picture that looks like what is seen from where you are sitting across the table from the learner.
- Have the learner move to that position and ask which picture matches the view from there.
Ask
- Which picture represents what you see from where you are sitting?
- Why?
- What picture do you think shows the way I would see the table from where I am sitting?
- Why? If answer and why is appropriate, then make a contradictory statement.
- Picture D is what would be seen from the position across the table (where I am sitting).
Assessment comments and suggestions
Egocentric point of view
- Matched their perception from their point of view (reference point) to select a matching representation.
Changes point of view, allocentric
- Remembers the position of three objects, conserves their relative positions as they mentally rotate their visual representation 90 & 180 degrees.
Developmental notes
Egocentric point of view
- Young learners are egocentric and do not recognize different points of view. One of the first situations in which they may recognize people can have different points of view is their likes and dislikes. Another situation is when viewing or listening to a story and begin to realize different characters have different points of view which is seen in the different ways they act. The wolf acts from the point of view of wanting to eat the three little pigs or grandmother and the pigs and Little Red Riding Hood act on their point of view of avoiding being eaten.
Changes point of view, allocentric
- If I stand in front of another person and we each raise our left hand, they do not match.
- My raised left hand in a mirror is on the right side of my image in the mirror. It's backwards.
- Uses logical reasoning to alter their visual perception from one point of view to a another by visually memorizing the position of the objects and rotating the visual representation of all three conserving their positions in a line and simultaneously rotating all three together 90 and 180 degrees.
- About fourth grade, children realize a description given to locate objects or places changes with a starting position or is relative t0 a point of reference.
- Visual spatial allocentric and egocentric point of view
- Activities on relative position & motion
Cars relative velocities activity (11 years)
Materials
Two toy cars and road map. 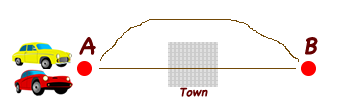
Directions
- Put the cars at position A.
- Tell the learner that the paper represents a map with two roads. One road going straight from A to B through the town (Trace the path). The other road going around the town from A to B (Trace the path).
- Tell her or him that both cars started from point A and arrived at point B at the same time.
- Ask how is that possible?
- Ask how do you know?
- If the answer and explanation are reasonable, make a contradictory statement.
Ask
- How is it possible both cars arrived at the same time?
- How do you know?
- If the answer and explanation are reasonable, make a contradictory statement.
- The car that traveled further didn't actually arrive at the same time. The car that went through town didn't have to stop for traffic lights so was able to go faster.
Assessment comments and suggestions
- Said both cars didn't arrive at the same time. Said the car that travels straight through town or has the shorter distance will arrive first.
- Said the car that went through town was slowed by traffic.
- Said one car went farther faster and the other went a shorter distance at a slower rate. Related distance and time to rate.
Developmental notes
- Decenters from the distance as the only variable that effects the outcome and operates on two variable, distance and rate, simultaneously to equalize time.
- Relates time and distance to rate. R = d * t.
- If the learner is asked to trace the paths with their index finger, will they trace it smoothly with both fingers arriving at point B at the same time? Or will one arrive before the other? Or will they motion be jerky and difficult for him or her coordinate the arrival simultaneously?
Classification, Seriation, inclusion
Same and different, match, and discriminate
Learners recognize similar sounds, sights, objects, and events from a very young age. Babies recognize their mother's voice at birth, faces weeks later, and various objects soon after. This recognition requires a perceptual memory be matched to a current perception of an external object or event being processed for comparison. This is done for recognition and labeling or naming objects or events. Later the process can be refined to match and discriminate sameness and equality of different objects and events where accuracy depends on the complexity of the objects and events similarity or dissimilarity.
Thus discrimination of similar and dissimilar sounds, sights, objects, and events depends on perception and matching and leads to classification.
Learner's what and why questions facilitate this ability and lead to activities such as:
- Reading. Particularly picture books and talking about the images.
- Sesame Street famed: One of these things doesn't belong ... Sample
One of these things is not like the others,
One of these things just doesn't belong,
Can you tell which thing is not like the others
By the time I finish my song?Did you guess which thing was not like the others?
Did you guess which thing just doesn't belong?
If you guessed this one is not like the others,
Then you're absolutely...right!
- Eye spy
- What's my rule?
- Find the pair
- Twenty questions.
- Name that tune.
Class inclusion Subsets of sets (6 years)
Materials
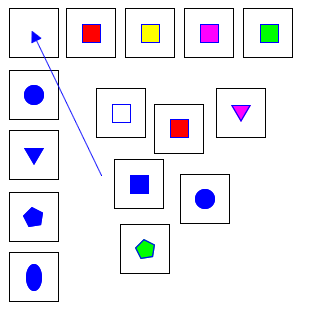 Three sets of cards. (Card sets)
Three sets of cards. (Card sets)
- One set of five cards with the same shape in five different colors (top row).
- One set of five cards with five different shapes in one of the same colors of the five different colors (left column).
- One set of cards with different shapes and different colors (stock set).
Directions
- Lay out the cards as in the illustration. Five cards with the same shape, but different colors in a row (minus the target card). Five cards with different shapes, but all the same color in an intersecting column (minus the target card). Mix the target card with cards of different shapes and colors to make the stock pile.
Ask
- What card can be placed here (point to where the empty square would be) so it matches (a property, characteristic, or attribute) in both rows?
- Why did you pick that card?
- If the card is correct (blue square) and reason is correct, then make a contradictory statement.
- The red square could go there also.
- The clear square ...
- The blue circle ...
Assessment comments and suggestions
Lacks inclusion
- Used one property to select (blue square, blue circle, white square, or red square) card. Selected correctly or incorrectly and stated the reason for the selection was based on one property, blue, square, or other shape or color. Not that two properties simultaneously were necessary for the selection.
Used inclusion
- Coordinated two properties simultaneously to select the appropriate card.
Developmental notes
- Centers on color or shape. Selects the blue square, blue circle, white square, red square. However, when gives reason doesn't mention two properties are essential for the selection.
- May believe that since blue are counted as blue, they can't be counted as squares (or vice versa) as as doing so would cause a double counting action, which isn't allowed when counting sets, because a one-to-one correspondence means to count each object only once.
- Decenters from the use of only one property and simultaneously uses two properties to classify objects.
- Classification misconceptions and concepts.
- Inclusion with the classification of animals activity
Simultaneous consideration of two properties activity (7 years)
Materials
Cubes or objects with three properties. Two different colors and same composition (plastic). 
Directions
- Lay out the checkers as in the illustration. Twenty checkers with the same shape and design, but two with different colors.
- Ask what color are the checkers, how many of each color, and what they are made of.
Ask
- What are the checkers made of?
- All of them?
- How many black checkers are there?
- How many red checkers are there?
- Are there more red checkers than black?
- Are there more plastic checkers or red checkers?
- Are there more red checkers or plastic checkers?
- Why?
- If the answer and reason is correct, then make a contradictory statement.
- If the black checkers are removed, then there will be more plastic checkers than red checkers.
- If I add two more red checkers, then there will be more red than plastic.
Assessment comments and suggestions
Lacks class inclusion
- Selected red.
Used class inclusion
- Selected plastic. Decenter from a strong visual perception, color to consider a second property, plastic, and realize both sets simultaneous have that property. They are simultaneously plastic and red, simultaneously plastic and black, and plastic is inclusive of all checkers.
Developmental notes
Lacks class inclusion
- Visual perception is a powerful impact on reasoning and overwhelms reason when more red is seen than black, which suggests there is more red if one centers on the property of color to arrive at an answer.
- Lacks action to decenter and consider another property (plastic) that coexists (simultaneous) with color (red and black). Class inclusion is not a relationship available to reason with and the visual color comparison is.
Used class inclusion
- Decenters from visual perception and considers multiple properties for individual objects and the possibility that another property can be included within more than one subgroup (color: red, black) or inclusive of the multiple groups.
- Classification misconceptions and concepts.
- Use of Venn diagrams is helpful to visualize the relationship and can be used to increase accuracy in classification and inclusion relationships.
Additional notes
- James McGarrigle created a different version of the simultaneous classs inclusion task with two properties.
- He used four toy cows, three black, and one white.
- He put all the cows on their sides, as if they were sleeping.
- Six year-old children were then asked:
- Are there more black cows or more cows?
- Then,
- Are there more black cows or sleeping cows?
Results: 25% percent of the children answered question 1 correctly, but 48% of the children answered question 2 correctly.
Discussion The process of laying the cows on their side increases the likelihood of more children focusing on that position as a stronger visual clue than the checkers being made of palstic in the above task (simultaneous consideration of two properties activity.
It supports the idea that children's visual perceptions are a major infuence on their thinking.
Seriation of length (7 years)
Materials
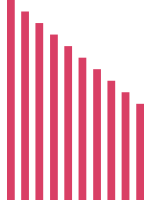
Ten wooden dowel rods or oak tag strips (about quarter inch (30 pixels) different lengths. If the strips are cut from paper they can be cut only on the left side of each strip, so the extra paper can be folded behind the colored strip to make each strip stiffer and easier to manipulate.
Directions
- Ask the learner to arrange the strips in order from short to long.
Ask
- Can you arrange these (hand strips to student) in order from short to long.
- Ask why they think they are in order from small to large.
- If the answer and reason is correct, then make a contradictory statement.
- If you move this one from here to here (point to one that is in order and to a position that would be out of order) they would still be in order.
Assessment comments and suggestions
Lacks seriation of length
- Placed the strips in a random order.
- Arranged them by comparing pairs. Pairs were arranged independently of the following or proceeding pairs.
- Compared one end of one strip to one end of another strip or to multiple strips without consideration of both ends of both strips so they were not seriated. Lined up all one end regardless of the other.
- Ordered several strips by comparing both ends simultaneously in their visual memory for a few comparisons, but not systematically. The series was partially or entirely completed in this way with a trial and error strategy, but no systematic efficient process.
Systematic seriation
- Systematically coordinated both ends of each strip to determine the lengths of the strips simultaneously across the whole set to seriate them systematically, efficiently, and accurately.
Developmental notes
Lacks seriation of length
- Randomly places the strips without consideration of any action or procedure that might be considered fair even if it would be inaccurate.
- Uses visual perception to estimate different lengths and a physical action to compare lengths. The action centers on aligning each strip in a fair manner without consideration of distance with respect to both ends simultaneously.
- Uses visual perception and a physical action to compare distance between both ends simultaneously for a few comparisons, but not systematically. Uses visual memory that can order two or three or more, but working memory becomes overwhelmed and falls short with no systematic operation.
- Recognizes length is conserved when the position of a strip is transformed and reversed. Uses physical actions to order a set by relating a first element to the second, second to the third, and so on and in the same way by relating the last element to the next to last, second to last to the third from last in the same way. With persistence may order all with trial and error, but has not developed a systematic operation to do so.
Seriation
- Seriates (order objects in a sequence). Systematically considers distance between both ends. Use a procedure such as: holding all the strips in one hand, allowing one end of all the strips to touch the desktop and pull them out in order from small to large. Recognize the ends determine the distance between both ends and simultaneously considers both ends to seriate objects by length.
- When they can seriate they will be able to do it without the objects being visible. For example seriate them behind a screen, or in a pillow case.
Simultaneous Relationships Brothers & Sisters activity (8 years)
Materials
Understanding their familial relationships.
Directions
- How many brothers and sisters do you have?
- What is a brother and sister?
- Tailor questions to the particular situation, like. How many brothers does [insert each member of the family] have? How many sisters does [insert each member of the family] have?
- Create a hypothetical family and ask the same set of questions. [Emma, Olivia, Ava, Noah, Jayden] How many brothers does (insert each name) have?
Ask
- How many brothers and sisters do you have?
- What is a brother and sister?
- How many brothers does [insert each member of the family] have?
- How many sisters does [insert each member of the family] have?
- How many children are in this family? [Emma, Olivia, Ava, Noah, Jayden]
- How many boys? What are there names?
- How many girls? What are there names?
- How many brothers does each child have? (Emma, Olivia, Ava, Noah, Jayden)
- How many sisters does each child have? (Emma, Olivia, Ava, Noah, Jayden) have?
- Emma has two sisters, Olivia and Ava. How many does Olivia have?
- Your brother has a sister so you must have a sister also.
- Your sister has a brother so you must have a brother also.
Assessment comments and suggestions
Did not recognize simultaneous familial relationships
- Didn't recognize familial relationships.
- Recognized familial relationships inside their family except their own relationship as a sister or brother to their brother or sister.
- Recognized familial relationships of families outside their family.
Recognized simultaneous familial relationships
- Recognized familial relationships for other families and their own. Including their own relationship as a sister or brother to their brother or sister.
Developmental notes
Does not recognize simultaneous familial relationships
- Early definitions of brother and sister is boy and girl respectively.
- Children can identify themselves as a brother or sister and know how many sisters and brothers they have about age four. However, they do apply the idea that one must have a brother or sister to be one until around age eight (simultaneity).
Recognizes simultaneous familial relationships
- Some people will argue as to whether the problem children have with simultaneous relationships is created with perception or language. Or could it be both depending on the situation and person?
- It seems when questions with family names are presented in a group: ... [Emma, Olivia, Ava, Noah, Jayden], children answer more accurately. However, when a name is separated: Emma has two sisters, Olivia and Ava, children answer less accurately. The difference between them is both a different language syntax and a different perception, created by the word Emma being several words removed from the other three. Either way, children need to construct an operation for dealing with the idea that a person can have a brother and sister and be a brother and sister simultaneously.
- Emma has two sisters, Olivia and Ava. How many sisters does Olivia have? Children will more likely answer one.
- There are three sisters Emma, Olivia, and Ava. How many sisters does Emma have? Olivia? Ava? Children will more likely answer two.
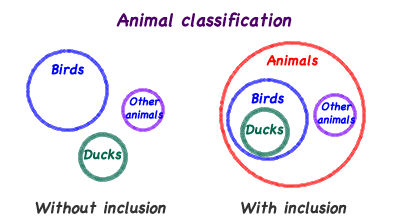
Class Inclusion Animals activity (7-16 years)
Materials
| Animal pictures to classify |for older students try a list of animals to classify |
 Directions
Directions
- Cut out the pictures and select the ones to give to learners to sort. Should include three or four animals for each category (ducks, birds, other animals). Ask the learner to sort the pictures into three groups. later may prompt her or him to make the categories of ducks, birds, and other animals. There are five different question sets for different ages of learners. Learners must be able to count the number of animals and identify the different kinds of animals. Decide which sets to use.
- Initial set up for all.
- Set one. For all to check for understanding.
- Set two (age 7)
- Set three (age 8)
- Set four four class inclusion (age 15)
- Set five (age 16)
- After the appropriate set ask why (reasoning) and if both OK, make a contradictory statement.
Initial set up directions to student. Say...
- Sort the pictures into three piles so each pile has a group of animals that could belong together.
- How many ducks are there? Are they in a pile of their own? If not put them there so I can ask some tricky questions.
- How many birds are among the rest of the animal pictures? Put them in their own pile.
- Put the rest of the animals in their pile. How many are left? (zero)
When the animals are in three groups ducks, birds, and other animals; then proceed to next set.
Question Set one to focus attention and check for initial understanding.
- How many ducks are there? (4)
- How many birds are there? (5 or 9)
- How many animals are there? (6 or 16)
Question Set two to see if learners reason with analysis (separate into groups or separate groups) and synthesis (combine into groups or combine groups) and if they consider two properties simultaneously. Notice if they use concrete or semi-concrete reasoning to analyze and synthesize the duck and bird pictures by physically moving them or mentally moving a visual representation to confirm their reasoning. Questionable use of class inclusion. (7 years)
- Suppose all the ducks went extinct (were all killed). Would there be any birds left? (yes)
- How do you know?
- If the answer and reason is acceptable, then make a contradictory statement.
Question Set three Use to see if inclusion is used to reason birds are included in the class of animals. Or birds are a subset of animals. Action or operation that considers two properties for one object simultaneously to compare to another group or set directly related (birds - animal). (8 years)
- In the whole world are there more birds or more animals?
- How do you know?
- If the answer and reason is acceptable, then make a contradictory statement.
Question Set four Use to see if inclusion is used to reason ducks are included in the class of birds and the class animals is inclusive of both. Or ducks are a subset of birds which is a subset of animals (indirectly related ducks - birds - animals). Action or operation that considers two properties for one object simultaneously to compare to another group or set in a hierarchy of three or more. (15 years)
- Can the ducks be put into the bird pile?
- Can all three piles be put into one big pile? (ducks, birds, animals)
- How do you know?
- If the answer and reason is acceptable, then make a contradictory statement.
Question Set five (class inclusion reasoning with hierarchical classification with conflicting images) (16 years)
- If the ducks are in one pile (4) and the birds in another pile (5), Are there more ducks or more birds?
- How do you know?
- If the answer and reason is acceptable, then make a contradictory statement.
- These are animals (point to non birds or all animals as appropriate) so there are (six or sixteen).
- All the ducks are gone so there are no birds left.
- Putting all the ducks in the bird pile and the bird pile in the animal pile means there are no ducks just birds and animals.
- If there were cards with fish, they could be put with the birds.
- If there were cards with fish, the fish cards couldn't be put with the animals.
Assessment comments and suggestions
- Visually recognized birds, ducks, and animals other than birds.
- Used perception of one property to compare different groups that were physically grouped together or not.
- Used inclusion to reason birds are inclusive in the class of animals.
- Used inclusion to reason ducks are included in the class of birds and the class animals is inclusive of both.
- Decentered from the visual prompt of more ducks than birds to recognize one group as inclusive of the other.
- Able to use inclusivity in a hierarchical situation three or more deep.
Developmental notes
- Uses perception inaccurately to compare groups and classify.
- Since the ducks are counted as ducks, they can't be counted as birds as double counting isn't allowed when counting sets, because of a one-to-one correspondence of count only once.
- Center on ducks as ducks and birds as birds and not birds as animals or ducks as animals. This is more obvious when young learners are shown a picture of eight fish and three turtles and asked. How many fish?(eight) How many turtles? (three) Are there more fish or animals? (fish). The learner focuses on the visual perception of all the fish. Doesn't decenter from the visual perception of fish and create a new visual perception of all animals in the picture, inclusive of fish and turtles.
- Reason with inclusivity. Reason ducks are inclusive of birds and birds are inclusive of animals, therefore ducks are inclusive of animals. Or reason that ducks are a subset of birds and birds are a subset of animals (subsets being inclusive of a larger set).
- Reason with hierarchical inclusion. For example, ducks are included in the class of birds and the class animals is inclusive of both. Or ducks are a subset of birds which is a subset of animals (indirectly related ducks - birds - animals). Action or operation that considers two properties for one object simultaneously to compare to another group or set in a hierarchy of three or more. Ducks and other birds = all birds. All birds - ducks = other birds. reversibility.
- More classification activities can be done with food (fruit, vegetables, meat, dairy ...) attribute blocks, people, ... Many classification activities open the door to controversy, such as is a tomato a fruit or vegetable, which allows practice for inclusion in multiple groups as well as a discussion that all classification is arbitrary and is only controlled by defining the classes.
Conservation
Overview of conservation, number conservation, & cardinality
To conserve means to recognize a property or characteristic of an object or group of objects that does not change when the object or objects are acted on in some way. Acted on can include actions such as left alone in time (also referred to as object permanence), moved, put in water, under go a shape change, and other actions.
Learners who do not conserve center on an irrelevant property and make comparisons relative to that property. Often influenced by their perceptual representation of that property without the use of logical reasoning. For example thinking six coins stacked up are less than six coins side by side in a row, by centering on the area the coins occupy instead of the number of coins being identical. Knowing the number of coins is conserved no matter how they are moved or arranged.
Thus, knowing when a property is conserved is important if a person is to reason in logical and accurate ways. Properties that are conserved in most situations are: shape, size, length, number, substance, weight, volume, area, mass, density, energy, and more.
Let me review the development of conservation of number.
Young learners use visual spatial representations of different groups of objects and compare them by matching them one-to-one or comparing the distance or area they occupy to determine which is more. This usually works when the number of objects is small, however, they do not conserve numbers as the number of objects increases or the distance they are apart from each other increases.
Conservation of number is first achieved with small quantities (1-3 and later maybe to seven). Next, they recognize equivalence when groups of objects do not change their position or the separate objects positions are not changed. Later, when a group of objects are moved place to place, and still later comparing two groups of objects that are spread apart or contracted in a row or in area the group occupies.
Young learners, who accurately determine equivalence of moved groups, decenter on the change of the positional spacing of the objects and recognize that operation has not acted in a way that would change the amount, therefore, the amount is the same (conserved).
Additionally they recognize when a group of objects positions are changed (transformed), it doesn't change the number of objects through out the entire transformation process. Which leads to understanding that a transformation can also be reversed to its original positioning and the value is maintained (conserved).
Conservation must be achieved and joined with cardinality before cardinality attains its ultimate value. Cardinality is the action of counting numbers being matched in a one-to-one relationship to a set of objects to determine the number value of the set. Conservation and cardinality together means the value of a set will not change no matter how the set is positioned or arranged and different kinds, shapes, sizes, ... of objects can be in sets of equal value.
Learners are amazed as they discover actions and procedures that are conserved. Learners who do not conserve believe values are changing when they are not, thus being confused when others assume they are conserving. This understanding can not be forced or told to young children. Learners need time to construct it so let them sleep on it and with more experience they will construct this understanding.
Learners have to and will develop this understanding for them self.
It is possible learners will accept what adults tell them and repeat it in very similar situations, as they want to please adults.
However, without their own constructions, they will fail in different situations. So relax, let them explore and manipulate objects in their world at their pace. Pose questions, make suggestions, and contradictory statements, but be ready to back off and let them work through their puzzlement as they construct their own understanding.
Equivalence of a set of objects (permanence conserved)
One-to-one Correspondence, and
Conservation of Number (7 years)
Activity 1 - Equivalence of a set of objects (permanence conserved)
Materials
Eight to twenty-three objects of the same shape and size, pocket or container to hold objects.
Directions
- Select a group of objects that the learner would consider a big number (8, 14, 16, 23).
- Have the learner determine how many they think there are (the exact value isn't necessary). Ask how many there will be if they put them in their pocket or the container. Have her or him put them in their pocket or container and ask how many are in her or his pocket or container. If they are the same number, ask, why, and if their answer is reasonable, make a contradictory statement.
Ask
- How many objects are there. The exact value isn't necessary.
- Put them in your pocket or container.
- How many are in your pocket or container? More, less, or the same?
- How many will there if you take all of them out of your pocket or container?
- Will there be more, less, or the same?
- How do you know?
- Contradictory statement if appropriate answer and reason.
- There are more objects in your pocket.
- If I put another object in your pocket there will still be ... (number of objects, 8 ... 23).
Assessment comments and suggestions
Lacks conservation of one-to-one correspondence
- Said the number of objects changed when they were moved.
Conserves one-to-one correspondence
- Conserved the number of objects as they were moved to and from different places.
- Said they were the same because there was no objects added or removed. They were just moved around.
Developmental notes
Lacks conservation of one-to-one correspondence
- Uses perception to think there are less or more objects because they are moved, scrunched together, or because they are theirs and they want more (egocentric).
Conserves one-to-one correspondence
- Uses logical reasoning to decenter from any perception that the number of objects decrease in number if they are clumped together in a pocket or increase when removed and spread out.
- Can decenter, use transformation, and reversibility to reason a group of objects are conserved as they are moved (transformed) into and out of the container or pocket (reversed) because none are added or taken away.
Activity 2 - One-to-one Correspondence &
Conservation of one-to-one correspondence for equivalence (7 years)
Materials
Eleven plastic or paper bowls and seven spoons (or forks and plates) 
Directions
- Tell the learner. Pretend we are going to get snacks ready for a group of people and I have these bowls (11) and you have these spoons (7). Hand the spoons to the learner. Don't mention the total number of either the bowls or spoons. Give a bowl to the learner and ask them to put a spoon in it. Continue for all the spoons (7) and place a spoon in each bowl until all seven are sitting in a row in front of the child. Set the remaining bowls aside if they are not already aside.
- Then ask. Are there more spoons or bowls in the row or are they the same?
- Take all the spoons and put them into one of the seven bowls, in the row and ask. Are there more spoons or bowls or are they the same?
- Ask why.
- If the learner answers they are the same and gives a reasonable explanation, then make a contradictory statement.
Ask
- Are there more spoons or bowls or are they the same?
- Move spoons.
- Are there more spoons or bowls or are they the same?
- How do you know?
- Contradictory statement if appropriate answer and reason.
- There are more bowls.
- If I put another spoon, there are still more bowls.
Assessment comments and suggestions
Lacks conservation of one-to-one correspondence
- Said there were more bowls than spoons. Appears to center on the visual space the bowls occupy to determine cardinality.
- Counted them and said they were the same.
Conserves one-to-one correspondence
- Said they were the same or there are as many bowls as spoons, because there were no bowls or spoons added or removed. The spoons were just moved.
- Said that there was a bowl for each spoon so they were the same (matched) and moving them didn't change that. Conserved a one-to-one correspondence.
Developmental notes
Lacks conservation of one-to-one correspondence
- Centers on visual perception to compare and concludes there are more bowls.
Conserves one-to-one correspondence
- Decenters from the visual perception of the larger space the bowls occupy and uses logical reasoning to counter their perception by operating on the spoons and bowls to maintain the one-to-one correspondence as they are transformed in space from their individual bowl to a collective bowl and realizes they can be reversed to their original position so equality or one-to-one correspondence is conserved. Or the number of bowls and spoons that are in a one-to-one correspondence is conserved when moved (transformed) and could be returned to the original positions (reversed).
Activity 3 - Conservation of number, one-to-one correspondence, equivalence (7 years)
Materials
Twenty to fifty similar objects or beans to make two groups of equal size.
Directions
- Decide on the size of the two equal groups of objects: 8, 12, 16, or 24.
- This example uses eight.
- Arrange 8 discs, or other small similar objects, in two horizontal rows in a one-to-one correspondence.
- Show the student the two rows of 8 objects and ask which has more objects.
- Rearranged one set so the objects are spaced farther apart over a larger area.
- Ask the learner which group has more objects.
- Ask how they know.
- Ask them why? Or to prove their answer.
- If the answer and explanation is reasonable, make a contradictory statement.
- If the learner is successful continue with a larger group.
- Alternative. Could start with the objects spread out in a one-to-one position and instead of spreading one row out further, slide it together.
- Switch rows and repeat.
 Ask
Ask
- Are the number of discs in each row the same or does one row have more than the other row?
- If the learner says they are the same, then spread one line of discs apart so it becomes a longer line. Or slide one row closer together so it becomes shorter.
- Ask the learner if there are more discs in one row than the other now or if they are the same.
- Ask the learner to explain why the rows are the same or different. (They are the same because you didn't take any away or add any. You just moved them or spread them apart).
- If the answers are correct and why is reasonable, make a contradictory statement.
- If we move a disc from this row (longer) to this row (shorter), then they will have the same number.
- This row is longer so it has more.
Assessment comments and suggestions
Lacks conservation of number
- Said the number of objects were the same to start and unequal when one row was moved, spread out or pushed together. Did not conserve number, or one-to-one correspondence, or equality or, cardinality.
Conserves number
- Said the number of objects were the same to start and stayed the same when one row was moved, spread out or pushed together. There were no objects removed or added to the either row. Conserved number, or one-to-one correspondence, or equality or, cardinality.
Developmental notes
Lacks conservation of number
- Centers on visual perception to compare the distance objects cover or area objects occupy and inaccurately concludes the number of objects in one row is different (more in longer, less in shorter) than the number of objects in the other row.
- Interestingly, learner's hand gestures will sometimes differ from the answers they give. For example: a learner who initially says the two rows are aligned or similar, before one row is moved, will answer that the one row covering more distance has more objects. However, their hand gestures will not agree. They will perform a gesture that is more towards similar rows than the rows where one row is longer than the other.
Conserves number
- Decenters on visual perception and uses logic to reason the perceptible difference of positions or different location of the objects does not change the number of objects. None has been added or removed, A one-to-one correspondence of objects in each row was conserved, equality was maintained, all conditions for cardinality were retained.
- It is possible the learner uses or conserves any one or combination of these relationships for these actions.
- Two groups of objects in a one-to-one correspondence can be moved (transformed) without changing their one-to-one correspondence or equality or cardinality. One-to-one correspondence of counting numbers to objects is the condition to determine cardinality. The depth of understanding can range from knowing a matched set of objects (sets with one-to-one correspondence) retains the match when they are moved (transformed) and returned (reversed). To equivalent sets retain their equivalence as they are moved (transformed) and returned (reversed). To a set of objects retains its one-to-one correspondence of counting numbers to objects when it is moved (transformed) and returned (reversed).
- See Number sense for ideas on development and activities to facilitate it.
Related task:
- In the Naughty Teddy task, created by James McGarrigle and Margaret Donaldson.
Children are shown two rows of counters with the equal amount of counters and asked if there is the same amount in each row. - Then a glove puppet (Naughty Teddy) messes up one row to make it look longer than the other.
- Then they are asked if there is the same amount in each row.
- Children performed better on this task than one without Naughty Teddy like in activity three.
Discussion The introduction of Naughty Teddy increases the likelihood of more children answering that the total number hasn't changed. It supports the idea that children who think about what happens when Teddy messes up the arrangement are using logical thnking and not relying on their viual perceptions.
Activity 4 - Conservation of Numbers, Different Sizes of objects (7 years)
Materials: 
Two sets of objects with very different size or different shapes to make double or triple sets of 7, 12, 16, & 23.
Directions
- Decide on the size of the equal groups of objects to use 7, 12, 16, or 23.
- Give the learner two sets where the number of objects are the same (7 objects) but the sizes and shapes are very different.
- Ask how the two groups of objects are alike and different.
- If the learner doesn't mention that the amount in each group is the same, then ask them to count each group.
- After they count the same number, ask if they are surprised that they were the same?
- Ask which has more or are they they the same amount?
- If answer and reason are accurate, make a contradictory statement.
Ask
- How are these groups of objects alike and different?
- If the learner doesn't mention the amount in each group is the same, ask them to: Count each group.
- Were you surprised they were the same?
- Which has more or are they the same amount?
- Why are they?
- If answer and reason are accurate, make a contradictory statement.
If the learner is successful, you may continue using
- the group of large objects and the mixed size objects and repeat the procedure.
- the group of small objects and the mixed size objects and repeat the procedure.
- a larger groups with equal objects of 12, 16, or 23.
- This amount is more, because the objects are so big.
- This amount is less because the objects are so small.
- If I take this big object and put it with the little, then they will be the same amount.
- If I take this little object and put it with the big, then they will be the same amount.
Assessment comments and suggestions
Lacks conservation of length
- Surprised and didn’t agree two groups both with 7, 12, 16, & 24 objects of different sizes had the same number of objects.
- Surprised and agreed they are the same. 7, 12, 16, 24, but did not give a reason or a logical reason why.
Conserves length
- Said the total amounts of different sized objects in two equal groups were the same (7, 12, 16, 24). Student conserved number.
Developmental notes
Lacks conservation of length
- Centers on visual perception of size, or area the objects occupy as changing the number value of a group.
- Centers on visual perception, is surprised, and agrees they are the same (7, 12, 16, 24). May be transitional as knows that number values relate to cardinality. However, still overwhelmed (centers) on position, size, area as a consideration for cardinality. Doesn't decenter and considers number of objects doesn’t change with a change in position, size, or shape with a prompt or by counting them. Doesn't seem to understand cardinality as the relationship of a one-to-one correspondence of numbers to objects.
Conserves length
- Is confident the number (7, 12, 16, 24) doesn't change with position, size or shape. Decenters and uses logic to operate on the objects with a one-to-one correspondence of numbers to objects irregardless of object's properties other than numerical comparison. Conserves cardinality of objects as they are transformed and reversed.
Conservation of Length Activities
Straws,
Yarn, and
Straws Zig-zag (7 years)
Activity 1 - Straws
Materials
Two straws
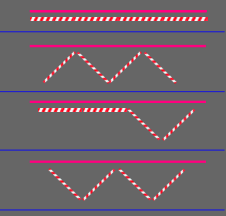
 Directions
Directions
- Place two straws parallel with both ends matching in length.
- Ask the learner if the straws are the same length or if one is longer.
- When the student agrees the straws are the same length, move one straws to the right or left.
- Ask which is longer.
- Move them back so they line up.
- Ask which is longer.
- If they agree both are the same length, move the other so the ends don't match the other.
- Ask which is longer.
- Move them back so they line up.
- Ask which is longer.
- If they agree both are the same length, move both so the ends don't match.
- Ask which is longer.
- If they still say they are the same length, then ask why.
- If answer is correct and the explanation reasonable, make a contradictory statement.
Ask
- Are the straws the same length or is one longer?
- Move one straw .
- Are the straws the same length or is one longer?
- Move straw back.
- Are the straws the same length or is one longer?
- Move other straw.
- Are the straws the same length or is one longer?
- Move both straws.
- Are the straws the same length or is one longer?
- Why?
- If the answers are correct and why is reasonable, make a contradictory statement.
- Move one straw in either direction farther and say, It is longer now.
Assessment comments and suggestions
Lacks conservation of length
- Said two straws have equal length when the starting and stopping positions are the same. Said two straws, of equal length, with different starting and stopping positions were not of equal length. Claimed one straw was longer or shorter than the other.
Conserves length
- Said the length of two equal length straws was the same irregardless of their position. Conserved length.
Developmental notes
Lacks conservation of length
- Centers on visual perception of different start and stop positions to compare length and inaccurately concludes length is different when it was not.
Conserves length
- Uses logical reasoning to counter their visual perception of an object's length (decenters) to identify two straws of equal length when their positions are and are not aligned.
- Compensates and determines length isn't effected (it's conserved) when straws of equal length change position.
Activity 2 - String (7 years)
Materials
Scissors, two pieces of string, yarn, or ...
Directions

- Place two pieces of string parallel with both ends matching in length.
- Ask the learner if the strings are the same length. If not, have them or you cut them until they are satisfied they are the same length.
- When the learner agrees the strings are the same length, move one string to the right or left.
- Ask if they are the same length or if one is longer.
- Move them back so they are lined up.
- Ask if they are the same length or if one is longer.
- If they agree both are the same length, then make one zig-zag so the ends don't match the other.
- Ask if they are the same length or if one is longer.
- Ask why?
- If the answers are correct and why is reasonable, make a contradictory statement.
Ask
- Are the strings the same length?
- Can you make them the same length.
- Are they the same length now?
- Move one.
- Are the same length or is one longer?
- Move them back.
- Are the same length or is one longer?
- Zig-zag one.
- Are the same length or is one longer?
- Why
- If the answers are correct and why is reasonable, make a contradictory statement.
- Move one string in either direction so they are farther apart and say. It is longer now.
- Straighten the zigzagging string and say it is longer now.
Assessment comments and suggestions
Lacks conservation of length
- Said the length of two equal length strings was the same length when they had the same start and stop positions.
- Said the length of two equal length strings was not the same length when the start and stop position was different.
- Said length of two equal length strings was not when the shape of string was different, straight vs. zig-zag.
Conserves length
- Said the length of two equal length strings were the same length when the start and stop position was different.
- Said the length of two equal length strings were the same length when the shape of the string was different, straight vs. zig-zag.
Developmental notes
Lacks conservation of length
- Centers on visual perception of two strings with equal length and the same starting and stopping positions and reasons they are the same length.
- Centers on visual perception to compare length and inaccurately conclude length is different when it is not.
- Perceives two strings of equal length with different starting and stopping positions as one longer or shorter than the other.
- Perceives two strings of equal length with one in a zig-zag position and one straight as one longer or shorter than the other.
Conserves length
- Decenters on visual perception and uses logical reasoning to counter visual perception of an object's length to reason the length of strings are the same when they are aligned with the same beginning and ending position or moved left or right to another position (transformed) or zigzagged (transformed) as they can be returned to the starting position (reversibility) to show their length has been conserved.
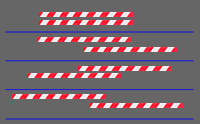
Activity 3 - Straws (7 years)
Materials
Four straws and one dowel (or stick) as long as the four straws end to end.
Directions
- Place the long dowel with four straws (end to end) below it.
- Ask which is longer or if they are the same length.
- Move the straws to make a smooshed letter M kind of design and ask if they are the same length or if the top one or bottom four are longer.
- Ask why and if answer is equal and reason reasonable, make a contradictory statement.
- Move the straws so two are end to end and two make a V design.
- Ask if they are the same or which is longer.
- Ask why and if answer is equal and reason reasonable, make a contradictory statement.
- Move the straws to make a letter W kind of design and ask if they are the same length or one is longer.
- Ask if they are the same or which is longer.
- Ask why and if answer is equal and reason reasonable, make a contradictory statement.
Ask
- Are the straws or the stick longer or are they the same length?
- Why?
- If the answer is equal and the reason reasonable, make a contradictory statement.
- Repeat...
- If I add another straw then they would be the same.
- If I straighten the zigzagging ones and move them to right, then the straws are longer.
- If I push the zig-zag closer together, then the stick will be longer.
Assessment comments and suggestions
Lacks conservation of length
- Said four straws end to end of equal length to a dowel were of equal length when the straws were end to end beside the dowel with their ends at the same starting and stopping points.
- Said the four straws (equal in length to the dowel) were shorter than the dowel when the straws were in a zig-zag pattern.
Conserves length
- Said the four straws (equal in length to the dowel) were of equal length to the dowel when the straws were in a zig-zag pattern. Conserved length.
Developmental notes
Lack conservation of length
- Centers on visual perception to compare length. Did not conserve length.
- Answers correctly when the start and stop position of the dowel and straws are the same. Visual perception suggests they are the same length. Says they are not equal lengths when the start and stop position are different. Such as when the straws are in a zig-zag pattern, which visually suggests the group of straws are shorter than the dowel.
Conserves length
- Uses logical reasoning to counter visual perception or inspection alone can be used to compare length of two or more objects (decenter). Centers on the lengths of straws not changing when their position changes (transformed). Can transform the position of the straws from along side the dowel to a zig-zag pattern while conserving their length and reversing them from the zig-zag positions back to their original positions along the dowel.
Conservation of substance, solid clay activity (7 years)
Materials
Two balls of clay or other modeling material.
- Directions
- Place two balls of clay on the table and have the student explore them.
- Ask the learner if the two balls have the same amount of clay (stuff, substance).
- If they agree continue. If not, ask them to pinch clay from one and move it to the other until they believe they are the same.
- Flatten one ball into a pancake and ask if they are the same now.
- Ask them to explain their answer or reasoning.
- Next, roll and stretch the pancake into a snake shaped object and ask if they are the same now.
- Ask them to explain their answer or reasoning.
- Roll the snake back into a ball and ask if they are the same now.
- Ask them to explain their answer or reasoning.
Ask
- After adjustment.
- Do they have the same amount of clay or does one have more?
- Flatten.
- Does one have more clay or do they have the same now?
- Why?
- If answer and reason is sensible, make a contradictory statement.
- Snake shape.
- Does one have more clay or do they have the same now?
- Why?
- If answer and reason is sensible, make a contradictory statement.
- If I flatten the pancake, then it will have more clay.
- If I stretch the snake further, then it will have more clay than the ball.
Assessment comments and suggestions
Lacks conservation of substance
- Said both amounts of clay were the same before the transformation, but not after one was flattened into a pancake shape and after it was rolled into a snake shape.
- Said both amounts of clay were the same before the transformation, said the clay was flattened into a pancake shape, but not when the clay was rolled into a snake shape.
Conserves substance
- Said both amounts of clay were the same before the transformation and after the transformation: flattened into a pancake shape and rolled into a snake shape.
Developmental notes
- Believed their visual perception of the solid taking up more table space, with the snake shape stretched longer or pancake shape flatter than the ball, is proof of more substance or solid matter.
- Perception of two lumps of clay, of equal solid amounts, with one being stretched longer than a second being more compact, would visually suggests the stretched has more substance and solid matter.
- Perception suggested the solid amount was different, but the individual believed the amount of clay was the same because none was removed or added to it when the shape was changed.
- Visual spatial reasoning was used to explain the solid matter was stretched into a different shape, that wasn't as compact, but clay was not added or removed. Shape is changed when it is transformed and reversed, but the amount of solid clay is conserved when it is transformed and reversed.
- Visual spatial reasoning could animate an explanation that show how the clay particles were being rearranged as the shape was changed, but the same number of particles or pieces of clay were maintained as it was transformed and reversed. See more later with conservation of volume.
Conservation of Salt or Sugar
Conservation of Substance (7 years),
Weight (9 years),
Volume (10 years) activities
The procedure can be used for three tasks (conservation of substance, weight, and volume) by changing the questions slightly.
Materials
Teaspoon of salt (Kosher salt will not cloud the water) or sugar, or sugar cube, two glass with the same amount of warm water.
Directions
- Have the learner compare the two glasses of water and have her or him make them the same amount of substance (pour & eyeball equal amounts), weight (use a scale), or volume (use a measuring cup or graduated cylinder) for the activity.
- Have the learner put the salt or sugar into one of the glasses and let it dissolve. If the water is stirred to hasten the process, use two identical spoons and stir each of the glasses with its own spoon. Ask the appropriate questions.
Ask
- Do both containers have the same amount of water. (If not make them the same.)
- Add salt or ... to one of the containers
- Is there still the same amount of water in each container or is there more or less?
- Are the water levels the same in each glass or is one higher or lower than the other?
- Select appropriate question for the activity
- Is the amount of salt the same in the glass as was in the teaspoon or is it more or less? (conservation of substance)
- Do both glasses weight the same or is one more or less than the other? (conservation of weight)
- Do both glasses have the same volume or is one more or less than the other? (conservation of volume) How much did the amount of salt water in the container change? Same as the amount (volume) or water, between the amount of water and salt added, or equal to the amount of water and amount of salt, or more than the salt and water combined? (conservation of volume)
- Why?
- If accurate and reason is reasonable, then make contradictory statement.
- If the same amount of salt was put in the other glass, then the amount would be heaver.
- If more water was added to the glass with the salt, then there would be even less salt.
- If two teaspoons of salt were added to this one, then it would still have the same amount as the other.
Assessment comments and suggestions
- Used perception to see the salt or sugar disappear, therefore, thought the substance, weight, or volume would change less.
- Used logical reasoning to counter their perception and reasoned that the salt and water were the same, no more water or salt was added or removed than the initial amount so the amount in the glass was equivalent to the original water and salt combined.
Developmental notes
- Reasoned the salt didn't disappear (conserved) and couldn't occupy the same space as the water, therefore, the volume had to increase relative to the amount of salt added.
Conservation of liquid (amount of liquid unchanged) activities
1. Direct method
2. Indirect methods: Measurement, & calculation of dimensions
Overview
Equivalence of volume can be reasoned with a direct method of moving a select volume from one place to another and indirect methods of measurement and calculation of dimensions (actual or imagined).
To understand and systematically explain how volume is conserved as it is transformed through space or transformed with a change of shape, a person must recognize which properties are effected and which are not. For example, dimensions don't change when a container with a certain volume is moved or rotated through space. And how dimensions do change when a liquid's shape changes (transforms) while its volume does not, it is conserved.
These changes can be animated concretely and semi-concretly with visual representations used in three basic ways to verify volume. 1. position is changed while dimensions are maintained reasoning dimensions determine volume, 2. position and dimensions are changed with volume reasoned by units of measurement, and 3, postion and shape is changed with volume reasoned by calculation with dimensions.
To conserve, a person decenters thinking about a singular visual spacial property. Such as how high or low the liquid appears in the containers. They recognize the amount of liquid as a property dependent on the three dimensions the liquid occupies. They know when a given amount of liquid changes shape (transformed) the amount of liquid remains the same (conserved). They might reason, none was added or removed; all the liquid was put into the other container, therefore, it is the same amount, as it was only moved from one container to another. They realize the amount can be returned to the original container (reversed) and the amount will be the same and have the same dimensions. A certain amount of liquid can be transformed from one shape to another and reversed to the original with the amount of water (volume) conserved.
When learners are asked what causes the shape to change. They will answer, that it just does, or say the glass makes it change, but may not accurately describe a systematic relationship between the dimensions of a shape and volume. That will come later as conservation of volume reasoned from units is used to build relationships of a shape's dimensions to its volume.
Let's look at examples for how conservation of volume can be verified:
First, position is changed while dimensions and shape is maintained 
Imagine a half gallon of milk upright and another on its side. Both with a half-gallon of milk. Now, imagine both of these two containers divided into units: 2 cubes x 4 cubes x 1 cube. These can be thought of container one: 2 cubes high x 4 cubes long x 1 cube wide and container two: 4 cubes high x 2 cubes long x 1 cube wide. If the first container is rotated 90 degrees, then it has the shape of the second. As it is rotated or animated, visualize each cube in each rectangular prism moving to where it would be positioned in the second. The dimensions can be said to change, but not the volume (volume is conserved).
As learners exerience this, reasoning will become almost automatic. However, before it does, learners will reason centered on one property and fail to conserve.
Second, position and dimensions are changed with volume verified by measurement
A specific volume put into two containers with different dimensions can be verified by remembering that two initial amounts were measured as an equal unit before being poured into two different containers. For example: container one: a cube 2 cubes high x 2 cubes long x 2 cube wide; and container two: 4 cubes high x 2 cubes long x 1 cube wide.
Another way to reason they have the same volume is to imagine how the dimensions of one container relate to the dimensions of the other. For example, the first container can be imagined to split in half from top to bottom and one half is move on top of the other half, then it will have the same dimensions of the second. Again each cube can be animated to visualize how each cube in the cube can move to make the rectangular prism. This is a bit more complicated, however, not impossible. It changes dimensions, but not volume (volume is conserved). Additionally each cube can be thought of a unit with both shapes having 8 cubic units.
Third, shape is changed and dimensions are used to verify volume
Formal operationally this is recognized as a function of size dimensions to volume. For example. A cylindrical container can be described with two dimensions: height of the container and radius of the bottom of the container. Volume is a function of height and pi times the radius squared (volume = h * π r 2). Therefore, if the height increases two times, then the radius would need to be decreased by half for the volume to be conserved. This too can be animated by simultaneously imagining the dimensions of a cylinder changing (diameter and height) and the volume flowing with the change from a short stout container to a tall slender container.
This becomes a bit more complicated if the container is a rectangular prism and all three dimensions are transformed simultaneously.
These explanations are complicated and require the construction of concepts that are not achieved until the middle grades. Do not force the issue. Let students sleep on it and with more experience they will construct this understanding. It is possible students will accept what adults tell them as they want to please them. However, if they have not constructed conservation, they will not be able to solve problems where conservation is necessary.
Indirect method measurement activities
Liquid amount not changed (conserved, not more or less) (7 years)
Materials
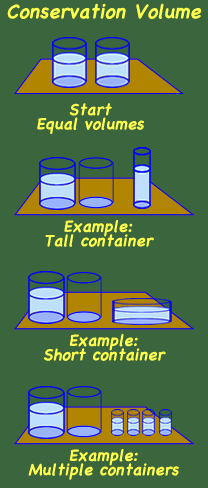
Two drinking glasses or containers with equal volumes of water, spoon or dropper, tall narrow container, short stout container, multiple small containers. All containers to visually suggest different volumes.
Directions
- Have the learner pour liquid into the glasses that are of equal volume.
- Ask the learner if the amount in each is the same or equivalent. If they say it isn't, ask them use a spoon or dropper to make them the same.
- Have the learner pour the amount from one of the glasses into the tall container.
- Ask if the amount in the other glass is the same as the amount in the tall container or if there is more or less.
- Ask why.
- If they answer the amounts are the same and provide a reasonable answer, then make a contradictory statement.
- Repeat the procedure with the short container.
- Repeat the procedure with the multiple containers.
Ask
- Is the amount in the glass the same, less, or more in that container?
- Why?
- If the answer is equal and the reason given is reasonable, make a contradictory statement.
- If I add more water to this glass, then there will be the same amount of water.
- If I take some water out of the glass, then there will be equal amounts.
- The water in the tall container is more than the amount in the stout container.
- All the water in these containers is more than in that one.
Assessment comments and suggestions
Lacks conservation of volume
- Said the amount of water changed when it was poured from one container to a taller or shorter container.
- Said the water was (more, less) when it was poured from one container to several smaller containers.
Conserved volume
- Said the volume of water does not change when it is poured from one container to another.
- Said the volume of water does not change when it is poured from one container to several containers.
- Said the volume of water does not change when it is poured from one container to another with different sizes and shapes or into several others with different shapes and dimensions because, a longer or shorter distance in one direction is compensated by a longer or shorter distance in the other direction.
Developmental notes
- Visual perception of the height of water in different containers is used to determine equal amounts of liquid volumes (centers on one dimension, usually height). Focus on height, suggests a taller container has a greater volume than a shorter one, or shorter container less less volume than a taller one, and containers of equal height have equal volumes.
- Visual perception suggests the volume of liquid is different, but the individual believes the amount of water is the same because it was measured and could be put back into the original container to prove it. Centered on one dimension, height, as reason for more, but is able to recognize that a liquid can be reversed or transformed back to the original container so it would be the same amount as at the start.
- Visual perception suggests a difference, but the student reasons if there was not a physical addition or removal of water, then the amount of water had to be the same. However, can not explain how a change in shape dimensions relates to volume.
- It should be noted. A direct method of conservation of volume does not require an explantion of the relationship of a shape's dimensions to its volume. It means a person can reason that a starting volume of liquid does not change (decenters on shape dimensions) when its shape changes (transforms), because it can be returned (reverses) to its original shape.
Conservation of liquid volume by its measured properties activity (7 years)
Materials
Large container with liquid, measuring cup, spoon or eye dropper, a drinking glass, tall narrow container, short stout container, multiple small containers. Containers with different dimensions. 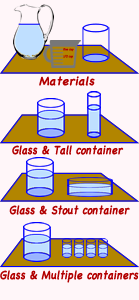
Directions
- Have the learner fill the measuring cup to 1 cup. Ask them if it is one cup. If not have them adjust it with the spoon or dropper until they are satisfied it is one cup.
- Then have them pour it into a regular glass.
- Repeat the process (measure 1 cup) and this time pour it into the tall container.
- Ask if the amounts in the two containers (glass & tall container) are the same or is one more than the other.
- Ask why?
- If the answer is equal and the reason reasonable, make a contradictory statement.
- Repeat the above process by replacing the tall container with the stout container.
- Repeat the process by replacing the stout container with four containers.
Ask
- Put one cup of liquid in the measuring cup.
- Does the measuring cup have one cup of liquid?
- Pour it into the glass.
- Does the glass have one cup of liquid?
- Put one cup of liquid in the measuring cup.
- Does the measuring cup have one cup of liquid?
- Pour it into the (tall, stout, multiple) container(s).
- Does the glass or the container have more, less, or the the same amount of liquid?
- Why?
- If the answer is equal and the reason reasonable, make a contradictory statement.
- If I add more liquid to this glass, then there will be the same amount of water.
- If I add more liquid to the (tall, stout, multiple) container(s), then there will be the same amount of liquid.
Assessment comments and suggestions
Lacks conservation of volume
- Said the tall container had more water.
- Said the glass had more water.
- Said the four containers had more water.
- Said the amount of water changed when it was poured from one container to a taller or shorter container.
- Said the water was (more, less) when it was poured from one container to several smaller containers.
Conserved volume
- Said the volume of water does not change when it is poured from one container to another.
- Said the volume of water does not change when it is poured from one container to several containers.
- Said the volume of water does not change when it is poured from one container to another with different sizes and shapes or into several others with different shapes and dimensions because, it was measured and there was not more water added or removed.
- Said the volume of water does not change when it is poured from one container to another with different sizes and shapes or into several others with different shapes and dimensions because, a longer or shorter distance in one direction is compensated by a longer or shorter distance in the other direction.
Developmental notes
- Learners center on their visual perception of one dimension of a container, such as being taller to determine volume.
- Perception cancels the act of measuring equal volumes of a liquid placed into containers with different dimensions, shapes. Used visual perception of one dimensions to ompare volume: one taller and narrower container than another, one shorter and stouter container than another, and a group of containers compared to one container.
- Perception suggested the volume of liquid was different, but the individual believed the amount of water was the same because it was measured and could be put back into the measuring cup to prove it.
- Abstract reasoning can be used to explain the representation of the two by imagining the tall one shrinking in height as it increased in girth to match the small stout container.
- Visual perception of the height of water in different containers is used to determine equal amounts of liquid volumes (centers on one dimension, usually height). Focus on height, suggests a taller container has a greater volume than a shorter one, or shorter container less less volume than a taller one, and containers of equal height have equal volumes.
- Visual perception suggests the volume of liquid is different, but the individual believes the amount of water is the same because it was measured and could be put back into the original container to prove it. Centered on one dimension, height, as reason for more, but is able to recognize that a liquid can be reversed or transformed back to the original container so it would be the same amount as at the start.
- Visual perception suggests a difference, but the student reasons if there was not a physical addition or removal of water, then the amount of water had to be the same. However, can not explain how a change in shape dimensions relates to volume.
- It should be noted. A direct method of conservation of volume does not require an explantion of the relationship of a shape's dimensions to its volume. It means a person can reason that a starting volume of liquid does not change (decenters on shape dimensions) when its shape changes (transforms), because it can be returned (reverses) to its original shape.
Conservation of solid volume by its measured properties activity (9, 11 years)
Materials
Number of cubes equal to three times the selected volume to match.
Directions
- Use the cubes to construct a rectangular prism that is 3 x 3 x 4 (volume of 36 cubes. Analogy a building with nine rooms per floor with four floors for a total of 36 rooms.
- Tell the learner that the building is a hotel with rooms and floors and how many rooms on each floor, how many floors, and how many rooms in the entire hotel.
- Check for understanding. How many floors? How many rooms on each floor? How many rooms in the whole building?
- Ask the learner to construct another building with the same amount of rooms, but with only six rooms on a floor?
- Ask, them how they know it has the same number of rooms.
- If their building is accurate and the reason reasonable, state a contradictory statement.
- Repeat with a base of 4 (2 x 2).
Ask
- How many floors?
- How many rooms on each floor?
- How many rooms in the whole building?
- Can you construct another building with the same amount of rooms, but with only six rooms on a floor?
- How do you know it has the same number of rooms?
- If the building is accurate and the reason reasonable, state a contradictory statement.
- Can you construct another building with the same amount of rooms, but with only four rooms on a floor.
- How do you know it has the same number of rooms?
- If the building is accurate and the reason reasonable, state a contradictory statement.
- If I add __ (insert number of cubes for another floor) more cubes on top, then it has the same number of rooms.
Assessment comments and suggestions
- Perception cancels the act of measuring equal volumes by counting cubes and stopping when the buildings (rectangular prisms) are equal height.
Developmental notes
- Abstract reasoning can be used to explain the difference in height by making and referencing that with less rooms on each floor, the building will need to be higher so they have the same number of rooms.
Conservation of area activity (9 years)
Materials
Two identical pieces of green paper, identical cubes, or Monopoly hotels to represent red barns, two cows or other grass eating animals.
Directions
- Act out the following story.
- Mr. Smith and Mrs. Jones. Both have a farm yard with the same amount of grass.
- Place two identical pieces of green paper.
- Ask, Does one farm yard have more grass or are they the same? (neither they are the same.)
- Okay good. Now on with the story.
- Mrs. Jones decides one day that it is time for her farm to grow so she builds a barn. Place one barn (Monopoly hotel) on the green paper.
- Mr. Smith, wanting to keep up with the Jones, builds a barn exactly the same size. Place another barn on the other green piece paper.
- The next year Mrs. Jones decides that things are even better and builds two more barns along side of the first barn. Place two more barns on the green piece of paper right beside the first.
- Mr. Smith, again wanting to keep up with the Jones, builds two more barns, but he spreads them out across the barn yard. Place two more barns on the green piece of paper so all three are spread around on the paper.
- The following year Mrs. Jones has another good year and builds two more barns again side by side her original. Place two more barns on the green piece of construction paper beside the other three.
- Again Mr. Smith, keeping up with the Jones, builds two more barns and again he spreads his barns out across his farm yard. Place two more barns on the green piece of paper spread apart from each other as much as possible.
- If there are more barns, I continue until all are placed on the green paper, making sure to add them equally.
- Then one day Mrs. Jones goes out and buys a cow.
- Mr. Smith, wanting to keep up with the Jones, goes out and buys a cow.
- When both cows are let out into the farm yards, which cow is going to have more grass to eat?
- Ask why.
- If the answers are correct and why is reasonable, make a contradictory statement.

- The cow in Mrs. Jones field will have more grass to eat.
Assessment comments and suggestions
Developmental notes
- Most people, when they experience this type of problem, will have as their first hunch or answer the cow in Mrs. Jones's pasture. The perception of all that green grass overwhelmingly influences their solution. The image of the red barns spread across the green paper and image of the green paper with barns huddled together in a corner can create a preoperational non-conservation of area response, or Mrs. Jone's cow has more grass, based on the visual evidence.
However, if you are skeptical enough or open-minded to ask yourself to just wait and think from another point of view. Then, you could reason the amount of green covered by the same number of barns is equal and each cow would have the same amount of grass.
If you are still not sure, act it out. Get two pieces of graph paper and color in squares for each barn. On the one sheet color them all in a corner and on the other spread them out. Is the area uncolored the same? Is the amount of grass the same. - In order for a person to conserve area he or she needs to be able to stop their egocentric thinking and consider how someone else might think about this problem differently than just by looking at it.
Decenter, how else can I think about this problem rather than by looking at the amount of green and comparing?
Transformation, think what would happen if all the spread out barns were brought together (transformed) to the grouped positions. Or what would happen if all the barns grouped together were transformed to the spread out position?
Their position doesn't effect the area they occupy. They are still sitting on the same about of grass.
Reversibility, if the barns are moved or spread out, then they can be returned to being together. In fact the process of moving the barns doesn't change the area they occupy, therefore there are an infinite possible number of places the barns could be positioned and the area would still be the same. Egocentric thinking is replaced by critical logical-mathematic reasoning. - Child used perception to compare ... and inaccurately concluded ...
- Child could used logic to reason the perceptible difference of the objects ... was not a condition of ...
Conservation volume and displacement.
Pancake snake, balls, metal sphere activities (14, 15 years)
Materials
Two balls of clay or other modeling material. One steel sphere or other metal ball heavier than the same volume of clay. Two identical containers of water with the same amount of water.
Directions
- Place two balls of clay on the table and have the learner explore them.
- Ask the learner if the two balls have the same amount of clay (stuff, substance).
- If they agree continue. If not, ask them to pinch clay from one and move it to the other until they believe they are the same.
- Show the learner the containers and have them verify the amount of water is equivalent.
- Flatten one ball into a pancake.
- Ask them to predict if one will raise the water more than the other or they will both raise it the same.
- Ask them to explain their answer or reasoning. If their answer and reasoning is accurate, then make a contradictory statement.
- Next, roll and stretch the pancake into a snake shaped object and ask if they are the same now.
- Ask them to predict if one will raise the water more than the other or they will both raise it the same.
- Ask them to explain their answer or reasoning. If their answer and reasoning is accurate, then make a contradictory statement.
- Next, break the snake into a 5-10 small spheres and ask if all the small spheres are the same as the big sphere now.
- Ask them to predict if one will raise the water more than the other or they will both raise it the same.
- Ask them to explain their answer or reasoning. If their answer and reasoning is accurate, then make a contradictory statement.
- Show the learner the metal sphere and ask them to make a clay sphere the same size. When they are satisfied they are the same size, ask which will raise the water level more.
Ask
- Which has more clay?
- Are they the same now?
- Is the amount of water the same in both containers? (If not adjust it so it is.)
- Predict if the sphere of clay or the pancake of clay will raise the water more or they will both raise it the same.
- Why? (If their answer and reasoning is accurate, make a contradictory statement.)
- Predict if the sphere of clay or the snake of clay will raise the water more or they will both raise it the same.
- Why? (If their answer and reasoning is accurate, make a contradictory statement.)
- Predict if the big sphere of clay or all the small spheres of clay will raise the water more or they will both raise it the same.
- Why? (If their answer and reasoning is accurate, make a contradictory statement.)
- Predict if the sphere of clay or steel sphere will raise the water more or they will both raise it the same.
- Why?
- If the answers are correct and why is reasonable, make a contradictory statement.
- If I flatten the pancake more it will take up more space and raise the water more.
- If I stretch the snake further, then it will have more clay than the ball and raise the water more.
Assessment comments and suggestions
- Believe their visual perception of the clay taking up more table space (as pancake or snake) is proof of more volume of solid matter, which will displace more water.
- Perception suggested the solid amount was different, but the individual believed the amount of clay was the same because none was removed or added to it when the shape was changed. However, believe the heavy steel sphere will displace more than clay of same volume.
- Visual spatial reasoning was used to explain the solid matter was stretched into a different shape, that wasn't as compact, but the amount of clay was not added to or subtracted from. Shape is changed when it is transformed and reversed, but the amount of solid clay or volume is conserved when it is transformed and reversed.
Developmental notes
- Reasoned the objects volume was not changed (conserved) as the shape was changed. Could use transformation to reverse the clay to its original shape, therefore it should displace equal amounts of volume, conservation of volume. (15) The transformation can be imagined with visual spatial reasoning as an animation that shows how the clay particles being rearranged as the shape changes with all the particles maintained as they are transformed from one position in the before shape to the after shape and reversed.
Displacement of liquid by mass and volume activity (13 years)
Materials
Liquid (water), two containers (small slender olive jars) to put sinking objects and mark the depth of water. Sinking objects cylinders or bolts or screws (at least three that are the same size, but different densities; and one that is the same density, length, but greater diameter. Sample set:
- 1 steel or chromium - two inches long 1/4 inch diameter,
- 1 aluminum - two inches long 1/4 inch diameter,
- 1 brass - two inches long 1/4 inch diameter,
- 1 steel or chromium - two inches long 1/2 inch diameter,
Directions
- Have the learner fill the two identical containers with the same amount of water.
- Have them pour water in or out till they agree the level of water is the same in both containers.
- Have the learner put one of the three matching bolts into one container.
- Have them select one of the remaining three to put into the second container and ask them if the level of water will be the same or more or less after it is put into the second container.
- Why do you think it will (insert student's answer)? If accurate answer and reason make a contradictory statement.
- Remove the bolt.
- Ask if the water levels are identical. If not have them adjust them till they agree they are.
- Ask the learner to repeat the procedure with each of the remaining bolts.
Ask
- Is there equal amounts of water in each container? Adjust till agree.
- Put this bolt into one of the containers.
- Select one of the other bolts to put in the other container and predict if the water level will be the same or more or less.
- Why?
- If the answers are correct and why is reasonable, make a contradictory statement.
- Repeat for the nest two ...
- These two together will raise the water level the same as that one.
- These three (same size different densities) will raise the water level differently.
Assessment comments and suggestions
- Predict the amount of water will rise according to the weight of the objects.
Developmental notes
- Used logical reasoning to decenter from weight of the objects when thinking about sinking and floating, and centered on the volume of the object that would displace or push the water level up.
Probability activity (11 years)
Materials
Bucket of cubes (96) of four different colors (36 red + 36 blue, 20 pink, 4 green), opaque sack for the cubes,
Directions
- Separate by color into four groups of 36 red, 36 blue, 20 pink, and 4 green.
- Then have the learner separate each color group in half (18 red, 18 blue, 10 pink, and 2 green).
- Ask if the two groups are exactly the same. If not adjust.
- Put one set into an opaque sack and set the other set aside as the reference set.
- Have the learner shake the sack. Tell her that she is going to pick two cubes from the sack without looking, but before she does, ask her to predict what colors might be selected.
- Ask her, why she decided on those colors? If probability was used and reason is reasonable, make a contradictory statement.
- Have her pick two without looking and place them on the table.
- Ask her to predict what the next two picks will be. Ask why. If probability and reason was used, then make a contradictory statement. May mention the reference set if she doesn't reference it.
- Then have her pick two, and place them on the table. If she doesn't sort them by color, suggest she does so as each is placed.
- Continue picking, asking for reasons, and throwing in a contradictory statement every once in awhile.
- Note the strategy the student uses and how she responds to the contradictory statements.
Ask
- Are these two groups (point to each group of [18 red, 18 blue, 10 pink, and 2 green]) exactly the same. If not adjust.
- Put one group in the sake & shake it.
- When you pick two what colors do you think they will be?
- Why? If probability was used and reason is reasonable, make a contradictory statement.
- Pick two cubes form the sack and put them on the table.
- What do you think the next two picks will be?
- Why? If probability was used and reason is reasonable, make a contradictory statement.
- Continue picking, asking for reasons, and throwing in a contradictory statement every once in awhile.
- I think the next one will be pink. I think the next one will be green.
Assessment comments and suggestions
- Predicted probability by guessing their favorite color or guessing the same color as the last one selected, or just guessing randomly.
- Predicted probability by using a strategy for guessing, but the strategy isn't probabilistic.
- Used the reference set to predict initial guesses and later adjusted picks by using number of cubes of each color drawn and using it to estimate a probability for the colors left by perceptually comparing the drawn set to the reference set.
- Used logical reasoning to systematically compare the reference set to the drawn set and estimate or calculate mathematically a probability to use to guess the next cubes drawn.
Developmental notes
- To use probability systematically she or he must be able to figure all the possible outcomes, which requires combinatorial representation, and to be able to compare each outcome or group of outcomes as proportions.
- Explanations of probability, experimental and theoretical in a teaching unit with an agenda for project based learning.
- More problems with teaching suggestions
Probability as proportion activity (12 years)
Materials
Opaque sacks for the cubes, bucket of cubes (168) of four different colors to make the following sets:
- 36 red + 36 blue, 20 pink, 4 green
- 18 red + 18 blue, 10 pink, 2 green
- 9 red + 9 blue, 5 pink, 1 green
Directions
- Have the learner separate the cubes by color into three sets
- Set A. four groups of 36 red, 36 blue, 20 pink, and 4 green
- Set B. four groups of 18 red + 18 blue, 10 pink, 2 green
- Set C. four groups of 9 red + 9 blue, 5 pink, 1 green
- Display in writing, pictures, sample sets or all.
- Put each set into a sack.
- Ask the student what two color cubes she thinks will be drawn from each sack if she randomly draws two from each sack.
- Ask her, why she decided on those colors? If probability was used and reason is reasonable, make a contradictory statement.
- Have her pick two form each sack without looking and place them on the table.
- Ask her to predict what the next two picks will be. Ask why. If probability and reason was used, then make a contradictory statement. May mention the reference set if she doesn't reference it.
- Then have her pick two, and place them on the table. If she doesn't sort them by color, suggest she does so as each is placed.
- Continue picking, asking for reasons, and throwing in a contradictory statement every once in awhile.
- Note the strategy the student uses and how she responds to the contradictory statements.
Ask
- What two color cubes do you think will be drawn from each sack if you randomly draws two from each sack?
- Why did you pick those colors? If probability was used and reason is reasonable, make a contradictory statement.
- Pick two form each sack without looking and place them on the table.
- What do think the next two picks will be?
- Why? If probability and reason was used, then make a contradictory statement. May mention the reference set if she doesn't reference it.
- Pick two, and place them on the table. If she doesn't sort them by color, suggest she does so as each is placed.
- Continue picking, asking for reasons, and throwing in a contradictory statement every once in awhile.
- Note the strategy the student uses and how she responds to the contradictory statements.
- I think the next one will be pink from this sack, green from this one, and green from this one.
- I think the next three will be green.
Assessment comments and suggestions
- Predicted probability by using a strategy for guessing, but the strategy isn't probabilistic.
- Used the reference set to predict initial guesses and later adjusted picks by using number of cubes of each color drawn and using it to estimate a probability for the colors left by perceptually comparing the drawn set to the reference set.
- Used logical reasoning to systematically compare the reference set to the drawn set and estimate or calculate mathematically a probability to use to guess the next cubes drawn. Recognized that sets A, B, & C are proportional and used that idea to make similar selections for each set adjust as the number of drawn colors changed the probability and proportions. Recognized that 4 green in set A was not more likely to be drawn than 1 green in Set C. Proportionally equal 4:96, 2:48, & 1:24.
Developmental notes
- To use probability systematically she or he must be able to figure all the possible outcomes, which requires combinatorial representation, and to be able to compare each outcome or group of outcomes as proportions.
- Explanations of probability, experimental and theoretical in a teaching unit with an agenda for project based learning.
- More problems with teaching suggestions