Pools & sidewalk tiles
Patterns & functions
Explore area, perimeter, tiling, & their relationships
Questioning is the foundation of all learning.
The first step in rejecting not knowing is to ask, why?
Sweetland
Overview
- Introduction
- Challenge - What's my pattern?
- Challenge - What's my equation?
- Hints
Introduction
This page explores area, perimeter, tiling, and the relationship between the length of the sides of pools and sidewalk tiles around them.
Challenge:
What's my pattern?
A landscaping architect is often asked to make pools with sidewalks around them. Often the client wants the pool to be square and the sidewalk tiles around it to be square.
The architect, asks you to draw some squares with sidewalk tiles around them to see what materials and costs would be needed as the size of the square inceased.
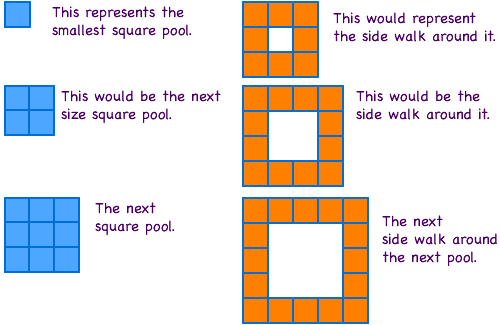
Questions:
What is a pattern for increasing the size of the pools?
What is the pattern for putting sidewalk tiles around a square pools?
Challenge:
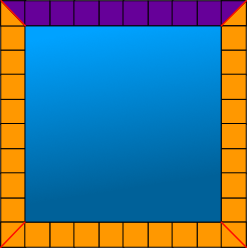
The picture below represents a koi pool. The water is shown in blue and the border in orange. This border has 10 tiles on one side. Determine the number of tiles in the border of the pool.

Write a formula or rule to use to determine how many squares the area of any sized square pool would be.
Write a formula, or rule, to use to determine how many tiles would be needed for a sidewalk around any sized square pool.
What relationships is there between the two?
Hints
Select a specific example to show what squares are represented in their formula or rule. When satisfied a rule or formula works, then generalize it for all different square pool sizes.
Think of repeated addition. When thinking of ways to represent multiplication, think of repeated addition (iteration of equal groups) instead of area, arrays, or matrices.
A couple of problems learners have include:
- Wanting to use multiplication (4 * 10) = 40
- Thinking of perimeter and wanting to add linear distances.
- Sometimes, using the linear side of the pool and adding 8 + 8 + 8 + 8 = 32 or (4 * 8 )
- Using the outside of the sidewalk and adding 10 + 10 + 10 + 10 = 40 or (4 * 10)
- Neither represents the number of square tiless around the pool.
Different ways to represent the number of tiles around a square pool with each side = to 8.
Eight whole tiles or squares and two halves = 9 tiles per side.
- ( 1/2 + 8 + 1/2) + ( 1/2 + 8 + 1/2) + ( 1/2 + 8 + 1/2) + ( 1/2 + 8 + 1/2)
- 4( 1/2 + 8 + 1/2)
- Generalize: with x being the length of a side of a square pool.
4(x + 1/2 + 1/2)

Eight tiles along each side of the pool and one at each corner.
- (8 + 8 + 8 + 8) + (1 + 1 + 1 + 1)
- 4(8 + 1)
- (4 * 8) + (4 + 1)
- Generalized: with x being the length of a side of a square pool.
(4 * x) + 4
Ten tiles along each side with two overlapping at each corner.
- (4 * 10) - 4
- Generalize: with x being the length of a side of a square pool. 4 (x + 2) - 4
Ten tiles on two sides and eight on two sides
- Generalize: with x being the length of a side of a square pool.
(2 * x) + 2(x +2)
Sharing multiple representations and their equations is helpful to construct accurate and deep knowledge about patterns, equations, area, perimeter, length, linear measurement,multiple perspectives, connections, algebra, geometry, how to generalize equations and patterns, and reversibility (by grouping or moving squares around to show how the different equations use the same number of orange squares and are therefore equivalent)
Create similar problems with pavers:
