Probability Unit:
Activity & lesson plans
- Big ideas, concepts, facts, & outcomes
- Content concepts, facts, & outcomes
- Process concepts, facts, & outcomes
- Attitudes
- Scoring guide suggestions
- Pedagogical overview
- Unit activities sequence
- Unit resources & materials
- Lesson plans
- Lab Notes
- Activity 1 - Probability of a one six-sided die
- Activity 2 - Probability of pulling different colors from socks
- Activity 3 - Probability and spinners
- Activity 4 - Probability of the sum of two six-sided dice
- Activity 5 - Probability of flipping two coins
- Activity 6 - Probability of how a cup lands when flipped and dropped
- Fact Sheets
Overview
A plan to review and facilitate deeper understanding of probability.
Activities include different experiments with a die, dice, and other probability events to conceptualize probability and how it can be determined experimentally and theoretically.
A plan designed for learners who have prior knowledge in
counting, basic operations, problem solving, classification, combinations, and other general math processes. This knowledge may be gained with participation in many math activities and units:
Background & related study topics resources:
- Classification - development & tasks
- Probability - development & tasks
- Probability & data analysis - list of activities & plans
- Probability concepts - in math knowledge base
- Spinners - activities, tree diagrams, spinner patterns & directions
- Math units & activities by dimensions
- Spinners & motion - activities for top like spinners & more
Discovery follow-up unit
- Carnival fun! - Includes an investigation with a reader's theater The Case of the Carnival Probability Game - Toss three coins. And other carnival problems with probability and combinations. With a learning agenda for problem based learning.
Intended learnings & learners thinkings
See for more information on what to include in planning
Big ideas, concepts, facts, and outcomes
Concept sequence map used for planning

Content concepts or outcomes
(Source concepts & misconceptions)
Big ideas and specific outcomes:
- Probability can be determined in one of two ways: theoretical and experimental.
- Theory is an idea used to explain or predict an event.
- Theoretical probability is determined with reasoning - by generating all the possible outcomes or combinations of outcomes in an event.
- Experiment is a test or set of trials made to try to understand something.
- Experimental probability is determined by repeating a certain event a number of times and collecting numerous results to determine the probability.
- Either way: the probability of an outcome is the number of specific outcomes out of the total number of all possible outcomes for a particular event.
Concepts and facts

Activity 1: Rolling one die.
- A six sided die has a one in six probability for each side.
- A fair die has equal probability for each side (Each number appears only once).
- (Generalization) The probability of an outcome is the number of specific outcomes out of the total number of all possible outcomes of one event.
- Theoretical probability is determined with reasoning.
- Experimental probability is determined by repeating a certain event a number of times and collecting numerous results to determine the probability.
Activity 2: Tiles in a sock - guess the populations colors
The probability of an outcome is the number of specific outcomes out of the total number of all possible outcomes of one event.
- Each sock has three tiles that are the same size, and one of three colors.
- Each tile has an equal chance of being drawn.
- The possible combinations are: all one color, two the same color and one different, three different colors.
- The more objects of one color, the greater the chance of that color being selected.
- The more trials, the more accurate the theoretical values that are obtained.
A prediction about a set (population) can be made from one or more samples.
- Each selection increases the possibility of selecting all tiles at least once.
- Predictions are derived from possibilities.
- Some possibilities have a better chance of occurring than others.
- Some possibilities are not likely to happen.
- Some possibilities are impossible to happen.
- Accuracy of prediction may be increased with more trials.
Activity 3:
Rolling and adding two six sided dice
- The probability of a certain sum of two die is equal to the total number different sum combinations for each possible sum out of the total number of all possible sums.
- Each die has six sides.
- Each die is the same.
- Each side has an equal chance of being rolled.
- Each die is fair.
- The sums of the die are: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
- There is one way for the dice to have a sum of 2, two for 3...six for 7 five for 8... For a total of 36.
- The probability of a specific outcome is equal to the total number of ways to achieve the same outcome out of all the total number of different outcomes possible.
- The probability of an outcome is the number of specific outcomes out of the total number of all possible outcomes of one event.
- Theoretical probability is found by generating all the possible outcomes or combinations of events.
- Theoretical probability doesn't usually match the experimental probability.
- Theory is an idea used to explain or predict an event.
- Experiment is a test made to try to understand something.
Outcome
Use and describe accurate procedures to determine theoretical and experimental probability for actual events by explaining probability as an outcome of the number of specific outcomes out of the total number of all possible outcomes of the one event.
- I can cause a certain tile to be selected. (think real hard, pick a certain way...).
- One tile always gets chosen more often.
- It is magic.
Young learners might look at their individual data and see the numbers are closer to the actual numbers, than the sum of all the class numbers and not see how the sum can be more accurate.
Process
Big ideas: Probability is determined by problem solving and reasoning to find possible outcomes and using representation to communicate proof for explanations to make predictions credible. See also Concepts & misconceptions
Related concepts and facts
- Problem solving
- Communication
- Representation
- Reasoning & proof
Outcome - Representation
Represents possible outcomes for an event.
Specific outcomes -
- Create a tree diagram to organize possible outcomes
Outcome - Communication
Communicates to seek solutions and reduce conflict.
Specific outcomes -
- See scoring guide for to communication to seek solutions and reduce conflict
Attitudes & dispositions
Big ideas: Value and seek to use mathematical understanding to explain the world. Persist in their curiosity to use logic and reasoning while working alone and cooperatively with others to derive usable explanations and procedures to solve problems. See math knowledge base for attitudes/disposition
Related concepts and facts
- Curious - Asks and answers questions to understand at deeper levels.
- Disposed to apply knowledge - Ready to think and apply what they know to current related experiences; all ideas from all dimensions (knowledge, processes, attitudes, and perspectives of science).
- Open-minded - Tolerates ideas and opinions of others and the importance of carefully considering ideas that may seem disquieting or at odds with what is generally believed and willing to change ideas in light of new evidence.
- Skeptical - Doubts, questions, and reconsiders conclusions based on evidence and reasoning.
- Tentative - Hesitant to draw conclusions.
- Reflective - Curious and willingly open-minded to consider new ideas based on evidence and reasoning against previous ideas based on evidence reasoning.
Outcome
Curious and open to possible explanations for observations. Is open-minded and skeptical to persist to find explanations, yet is reflective and tentative to definite solutions without sufficient proof.
Specific outcomes -
- Curious - Asks and answers questions to understand at deeper levels.
- Disposed to apply knowledge - Thinks and applies what they know to current related experiences; all ideas from all dimensions (knowledge, processes, attitudes, and perspectives of science).
- Open-minded - Tolerates ideas and opinions of others and the importance of carefully considering ideas that may seem disquieting or at odds with what is generally believed and willing to change ideas in light of new evidence.
- Skeptical - Doubts, questions, and reconsiders conclusions based on evidence and reasoning.
- Tentative - Hesitant to draw conclusions.
- Reflective - Curious and willingly open-minded to consider new ideas based on evidence and reasoning against previous ideas based on evidence reasoning.
Scoring guides suggestions (rubric)
Decision making skills to enhance health (scoring guide)
Top level
- Explain how to find experimental probability and theoretical probability for problems such as: Sums of dice with the number of sides different than six. Sums of dice with two different number of sides. Spinners with unequal partitions and or different colors of sections and the probability of getting pairs of colors.
- Select from scoring guide below
Lower level
Probability Development- scoring guide or rubric
Kind of reasoning Kind of task |
Transductive low level |
Transitional middle |
Generative upper |
Relational thinking top level |
|---|---|---|---|---|
| Thinking and reasoning | Uses irrelevant reasoning (Because I like red, 7 is my favorite number, 6 because it did 7 last time and it's going down, maybe it takes turns). | Uses concrete symbolic reasoning, generally along one aspect. When pressed will revert to transductive reasoning | Lists outcomes experimentally and with combination strategies that are coordinated and quantifiable. Reasons with the recognition of more than one feature. | Makes precise connections between sample space, outcomes, and their probabilities. Use valid numerical patterns to describe the probabilities of events and conditional events |
| Identification of possible outcomes | Lists an incomplete set of outcomes for simple problems. Simple problems include experiments of one task with one set (one die, one spinner, choosing marbles from one sock). | Lists a complete set of outcomes for a one task one set experiment and sometimes lists a complete set of outcomes for a two task experiment (sum of two dies, sum of two spinners) with limited and unsystematic strategies. | Consistently lists the outcomes of a two task experiment using a partially generative strategy. | Uses a systematic generative strategy that enables a complete listing of the outcomes for multiple task cases. |
| Statements of probability | Makes predictive statements with wording of most and least likely for events with subjective reasoning. Recognizes certain and impossible events. | Makes predictive statements with wording of most and least likely for events based on quantitative reasoning, but may revert to subjective reasoning. Recognizes certain and impossible events. | Makes predictive statements with wording of most and least likely for events based on quantitative reasoning including situations involving noncontiguous outcomes. Uses numbers informally to compare probabilities. Distinguishes certain, impossible, and possible events, and justifies choice quantitatively. | Makes predictive statements with wording of most and least likely for events based on quantitative reasoning for single task experiments. Assigns a numerical probability to an event as either a real probability or a form of odds. |
| Comparing probabilities | Compares probability of an event in two different sample spaces using subjective or numeric reasoning. Can not distinguish "fair" probability situation from "unfair". | Makes probability comparisons on the basis of quantitative reasoning (may not quantify correctly and may have limitations where noncontiguous events are involved) Begins to distinguish fair probability situations from unfair. | Makes probability comparisons on the basis of consistent quantitative reasoning. Justifies with valid quantitative reasoning, but may have limitations when non - contiguous events are involved. Distinguishes fair and unfair probability generators on the basis of valid numerical reasoning. | Assigns numerical probability measures and compares events. Incorporates noncontiguous and contiguous outcomes in determining probabilities Assigns equal numerical probabilities to equally likely events Probability comparisons are the ordering of the possibility of events happening. |
| Identify conditional probability | Does not give a complete list of outcomes even if a complete list was given prior to the first trial. Recognizes when certain impossible events arise in non replacement situations. | Recognizes probabilities of some events change in a non replacement situation (as marbles are taken from a sock and not replaced before next draw) however, recognition is incomplete and is usually limited to events that have previously happened. | Can determine changing probability measures in a non replacement event. Recognizes that the probability of all events change in a non replacement event. | Assigns numerical probabilities in replacement and non replacement situations. Distinguishes dependent and independent events. Conditional probability is the possibility of an event based on certain conditions. |
Social interactions in a conflict situation (scoring guide)
Top level
- Upper level: Social interactions recognize a conflict between subconscious influences and logical consequences and identify multiple ways to resolve conflict with respect to accept each person's individual rights of assertion, and use appropriate social skills when focusing on and stating the problem, analyzing the problem, stating alternative options and choices with positive and negative consequences, and communicating decisions that most individuals accept.
- Middle level: Social interactions seem to recognize a conflict between subconscious influences and logical consequences while recognizing different ways to resolve conflict and attempt to solve problems with regard to individual rights of assertion and use of applicable social skills to make or accept a decision that most individuals can accept.
- Low level: Social interactions seem to be driven by subconscious emotional influences in a manner that suggests decisions are based on influences for immediate personal or social outcomes and rewards, without regard to individual rights, concern for conflict resolution, or use of applicable social skills.
Lower level
Strategies to achieve educational learnings
Based on learning cycle theory & method
Instructional Procedure
Pedagogical Overview
Activities Sequence to provide sufficient opportunities for students to achieve the targeted outcomes.
Make sure learners have the prior knowledge identified in the background information.
- Activity 1 - Probability for a six sided die
- Activity 2 - Probability of pulling different colors from socks
- Activity 3 - Probability and spinners
- Activity 4 - Probability of the sum of two six-sided dice
- Activity 5 - Probability of flipping two coins
- Activity 6 - Probability of how a cup lands when flipped and dropped
Focus question
Unit focus question:
How do you predict the outcomes of different events (mathematical probability)?
Sub focus questions:
- What is probability?
- How do people make decisions about the likelihood of events?
- What do we mean whne we say something is impossible, possible, likely, unlikely, or certain?
- Events can be predicted as: impossible, possible, likely, unlikely, or certain. What percent can be associated with each?
Resources and Materials
- Lab notes
- Activity 1 - Probability of a one six-sided die
- Activity 2 - Probability of pulling different colors from socks
- Activity 3 - Probability and spinners
- Activity 4 - Probability of the sum of two six-sided dice
- Activity 5 - Probability of flipping two coins
- Activity 6 - Probability of how a cup lands when flipped and dropped
- Fact sheets
- Word bank
- Background & related study resources
Lesson Plans
Activity 1 - Rolling one die

Materials:
Focus questions:
- How do you predict the outcomes of a die toss?
Learning outcomes:
- Accurately predict the outcome of a fair die with any number of sides.
Suggested procedures overview:
- Put students in groups, focus their attention, and assess their initial understanding of the focus questions.
- Roll one die 36 times.
- Chart & discuss results.
- Describe theoretical and experimental probability for the die.
- Complete notebook.
Exploration activity
- Hold up a six sided die.
- Ask. What number do you predict I will get when I toss the die?
- What would you predict the outcome would be if we rolled this die 36 times?
- Ask. How did you arrive at your prediction?
- Record all answers on the board.
- Ask. What makes you believe they are right?
- Put students in groups of two or three and have them roll a die thirty-six times and collect the data.
Invention activity
- Bring the class together.
- Ask. How should we display our data.
- If students do not know how to arrange data, have them chart the number of rolls for each roll 1 - 6 (1 - 6 horizontal axis, # rolls vertical axis).
- Record their data on the board.
- Analyze the data.
- Ask.
- What number turned up most?
- What number would you predict would turn up most if you did it again?
- What are the odds of a certain number turning up?
- What did you discover from the data?
- Tell:
- The explanation you made before you rolled the die to describe your prediction is a theoretical probability.
- The explanation based on the data we collected is an experimental probability.
- The probability that each of six numbers has an equal chance or 1 in 6 probability of happening is based on the idea there are six different outcomes and each has a 1 in 6 chance of happening.
- Have students communicate what they learned in their math notebook. Require at least two explanations.
Discovery
- Ask. What would happen if they rolled different die with different amounts of sides?
- What if you had a spinner with four equally distributed colors of red, blue, green, and yellow?
- What if they had a sock drawer with three white and three black socks?
- What would happen if you rolled two die and added the dots?
Activity 2 - Tiles in a sock
Materials:
Prepare one sock for each group so each has three tiles that are the same size, and one of three colors. The possible combinations are: all one color, two the same color and one different, three different colors.
- Group (sock), three colored tiles, graphing supplies, pencil, paper, and a display board for the entire class.
Focus questions:
- Can you predict what the population of tiles in a sock without dumping all of the objects?
Learning outcomes:
- Make a specific number of random selections with replacement and draw a conclusion about the tile population of tiles in a sock.
Suggested procedures overview:
- Put students in groups, focus their attention, and assess their initial understanding of the focus questions.
- Draw one tile from a sock with three colored tiles.
- Chart & discuss results.
- Identify possible outcomes and the number of possible combinations.
- Draw four times from a sock with three colored tiles.
- Chart & discuss results.
- Identify possible outcomes and the number of possible combinations.
Exploration activity
- Ask.
- Can you predict what the population of tiles in a sock without dumping all of the objects?
- Record all ideas on the board.
- Ask.
- Why do you think their answer are good ones.
- Ask. Would you like to try?
- Show the socks and explain each sock tiles selected from identical colored tiles. (You may or may not want to mention what colors were used or wait, to add suspense, till they draw them from the socks.
- What would you predict is the color of each tile in the sock population?
- Do you think you can figure it out without looking or dumping them out?
- Group learners into groups of three.
- Outline the following directions on the board.
- Each group will rotate the following roles: selector, counter, recorder.
- Selector: Draws one tile from the sock, announces its color, returns the tile to the sock, and shakes the sock.
- Counter: Keeps track of the number of trials the selector has taken.
- Recorder: Records the color of each tile on the group paper.
- Selector: Returns the tile to the sock.
- Each person selects a tile four (4) times.
- Each group thinks about, discusses the results, then writes a group prediction of the sock population.
- Ask. Repeat the instructions.
- Complete the task.
- Cruise the room and observe interactions, note critical comments, answer questions about procedures, and make sure groups record the necessary information.
Invention activity
- Display data so all can view.
- If students do not know how to arrange data, suggest ...
- To record the number of each color drawn from the sock. Write each groups name horizontally, with each color above or below, and the number of times a certain color was drawn above or below the color.
- Have all groups put their data on the chart.
- Have each group explain how they arrived at their predictions.
- Ask or lead to ...
- More draws (data) would help to obtain a more accurate prediction.
Second exploration
- Students repeat the process with four more draws.
- Ask. Do you think additional draws will help?
- Record all ideas on the board.
- Ask them to explain how they think their answer is a good one.
- Ask if they would like to try four more draws.
- Remind them about the roles listed on the board.
- Check for understanding.
- Students complete the task.
- Cruise the room and observe interactions, note critical comments, answer questions about procedures, and make sure groups record the necessary information.
Second invention
- Ask. How can we display the data?
- If students do not know how to arrange data.
- Suggest they could add it to the previous.
- Could use different symbols of colors for the different trials.
- Students put their data on the chart.
- Ask. Would you change your predictions, based on additional data?
- Explain how they arrived at their predictions.
- Have the students explain the chart.
- Decide if another round would is necessary.
- Predict the probability for different combinations of tiles in the socks.
- Show students a sock and putting 2 red, 1 blue, and 4 yellow into the sock. Then have students write their predictions and explanations for what colors would be most and least likely be drawn.
Discovery
- Move to next activity with spinners.
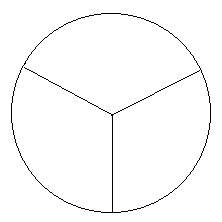
Activity 3 - Spinners
Materials:
- Card board to make spinners
- See motion and spinners unit
Focus questions:
- How do you make a fair spinner with three different results?
Learning outcomes:
- Describe what makes a fair spinner.
Suggested procedure overview:
- Put learners in groups, focus their attention, and assess their initial understanding of the focus questions.
- Design spinners.
- Ask. What did you base your design? theoretically and experimentally.
- Identify all possible outcomes and the number of possible combinations.
- Describe theoretical and experimental probability for the experiment.
- Complete notebook.
Exploration activity
- Put students in groups of two or three.
- Ask. What makes a spinner fair?
- Record all suggestions on the board.
- Ask. How will you design your spinner?
- Is your conclusion based on an experimental or theoretical idea?
- If your design is based on theoretical thinking, then ...
- Ask. What would you need to do verify it experimentally?
- Have the learners make and test their spinner.)
Invention activity
- Ask. How should we display the data.
- If learners do not know how to arrange data, suggest they chart the number of colors for each color on a spinner.
- Have each group display their data for the class.
- Ask.
- What pattern do you see from the data?
- What color turned up most?
- What are the odds of each color turning up?
- Analyze the data by having learners explain the pattern.
- Decide which of the spinner designs is most fair.
- Discuss how it might be fair theoretically, but not experimentally?
- Have learners communicate fair pattern and compare the experimental probability with the theoretical probability.
- Complete their notebook.
Discovery
- Review. We have explored rolling a fair die and spinning a fair spinner. You have also explored different colors of tiles in a sock. Can you think of different ways that dice are used in gaming? Next we will explore rolling two dice.
Activity 4 - Rolling and summing two die
Materials:
- two six-sided die, pencil, paper, notebook
Focus questions:
- What do you predict as the outcomes of a two die roll?
Learning outcomes:
- Determine the probability of the different sums (outcomes) of rolling two fair six-sided dice.
Suggested procedures overview:
- Put students in groups, focus their attention, and assess their initial understanding of the focus questions.
- Roll two six sided dice thirty-six times, find their sum, record and chart the results.
- Chart & discuss results.
- Identify all possible outcomes and the number of possible combinations.
- Describe theoretical and experimental probability for the experiment.
- Complete notebook.
Exploration activity
- Put learners in groups of two or three.
- Ask. What outcomes would you predict if you tossed two six sided dice at a time, summed them, and repeated it 36 times?
- Record all suggestions on the board.
- Ask. How did you determine your prediction?
- Is your prediction experimental or theoretical?
- Ask. What would you need to do to make an experimental prediction?
- Have the learners roll two dice 36 times and record the sums for each roll. (Or other appropriate experiment suggested.)
Invention activity
- Ask. How should we display the data.
- If learners do not know how to arrange data have them chart the number of rolls, vertically, as addends for each sum 2 - 12 horizontally.
- Roll the dice and collect the data.
- Have each group display their data for the class.
- Ask.
- What pattern do you see from the data?
- What sum turned up most?
- What are the odds of each sum turning up?
- Analyze the data by having students explain the pattern. It is necessary to list every pair of addends for each sum 2 - 12 theoretical probability.
- Have learners communicate the pattern and compare the experimental probability a theoretical probability.
- Complete their notebook.
Discovery
- Ask. What sum would you predict would turn up most if you did it again?
- What would happen for dice with different amounts of sides?
- What would happen with spinners that have different sized areas of colors on different spinners?
Activity 5 - Flipping coins
Materials:
- two or three coins, pencil, paper, notebook
Focus questions:
- What do you predict as the outcomes for flipping two or more coins?
Learning outcomes:
- Determine the probability of the different combinations (outcomes) of flipping two two or more coins.
Suggested procedures overview:
- Put students in groups, focus their attention, and assess their initial understanding of the focus questions.
- Decide how many times to flip the coins (50).
- Flip coins and collect the data.
- Chart & discuss results.
- Identify all possible outcomes and the number of possible combinations.
- Describe both theoretical and experimental probability for the exploration.
- Complete notebook.
Exploration activity
- Put learners in groups of two or three.
- Ask. What outcomes would you predict if you flipped two or more coins?
- Record all suggestions on the board.
- Ask. How did you determine your prediction?
- Is your prediction experimental or theoretical?
- Ask. What would you need to do to make an experimental prediction?
- Have the learners experiment and collect data.
Invention activity
- Ask. How should we display the data.
- If learners do not know how to arrange data have them chart the kinds flip outcomes and the numbers of each.
- Have each group display their data for the class.
- Ask.
- What pattern do you see from the data?
- What combinations turned up most?
- What are the odds of each turning up?
- Analyze the data by having learners explain the pattern. List every possible combination to verify theoretical probability.
- Have learners communicate the pattern and compare the experimental probability a theoretical probability.
- Complete their notebook.
Discovery
- Ask. Can you create a theoretical and experimental probability for the outcome of dropping a paper or plastic cup?
Activity 6 - Dropping or flipping cups
Materials: 
- paper or plastic cup, pencil, paper, notebook
Focus questions:
- How can you create a theoretical and experimental probability for the outcome of dropping a paper or plastic cup?
Learning outcomes:
- Determine the theoretical and experimental probability for the outcome of dropping a paper or plastic cup.
Suggested procedures overview:
- Put students in groups, focus their attention, and assess their initial understanding of the focus questions.
- Challenge the learners to create a plan to determine a theoretical and experimental probability for the outcome of dropping a paper or plastic cup.
- Plan.
- Share plans.
- Collect necessary the data.
- Chart & discuss results.
- Identify all possible outcomes and the number of possible combinations.
- Describe both theoretical and experimental probability for the exploration.
- Complete notebook.
Exploration activity
- Put learners in groups of two or three.
- Ask. How can you create a theoretical and experimental probability for the outcome of dropping a paper or plastic cup?
- Record all suggestions on the board.
- Let groups select and modify plans for both theoretical and experimental probabilities.
- Finalize plans.
- Implement plans.
Invention activity
- Ask. How should we display the data.
- Have each group display and explain their data to the class.
- Let each group decide to start with either theoretical or experimental probability and explain how they determined it.
- What data did you use to get the experimental probability?
- What reasoning did you use to get the theoretical probability?
- What makes you confident in each or not?
- Complete their notebook.
- Complete their notebook.
Discovery
- Ask. What other events can you use theoretical and experimental probability to better understand?
Lab Notes for activities
Activity 1 - Probability - six sided die

Materials: die, pencil, notebook
- Roll the die 36 times and record the results.
Chart the data
Summarize the class data.
What did you learn about probability of one die?
Describe a theoretical probability
Describe an experimental probability
What else did you learn?
Activity 2 - Probability of pulling different colors from socks
Materials: sock, tiles, pencil, notebook
Draw a tile from a sock, record the color, return it to the sock, repeat three more times.
Data
Summarize the class data.
What did you learn about the color of the tiles that might be in the sock?
Repeat
Data
Summarize the class data.
How did what you learned about the color of the tiles change?
Are your conclusions based on a theoretical or experimental probability?
What else did you learn?
Activity 3 - Probability and spinners
Materials: spinner, pencil, notebook
Design a spinner that will have equal probability of landing on three different colors.
Design
Describe the theoretical probability you used to create your design.
Experiment with the design and collect data to suggest the theory is appropriate.
Summarize the class data.
What did you discover?
What else did you learn?
Activity 4 - Probability of the sum of two six-sided die
Materials: die, pencil, notebook
- Roll two die 36 times and record their sums.
Chart the data
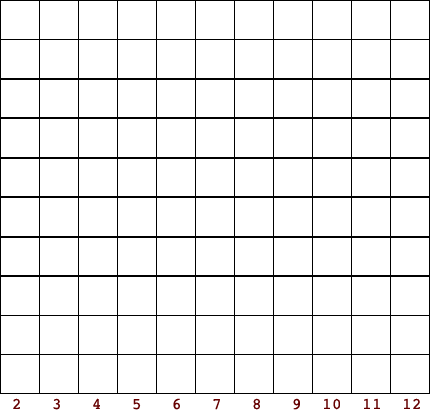
Summary of ways to sum two die:
2
3
4
5
6
7
8
9
10
11
12
Summarize the class data.
Activity 5 - Probability of flipping two coins
Materials: coins, pencil, notebook
Write a procedure to determine the theoretical and experimental probability of flipping two or more coins together. Can start with either one. Your choice.
Describe the theoretical probability
Reasoning
Describe an experimental probability
The data
Summarize the class data.
What did you learn about probability?
What else did you learn?
Activity 6 - Probability of how a cup lands when flipped and dropped
Materials: cup, pencil, notebook
Write a procedure to determine the theoretical and experimental probability of a flipped or dropped cup. Can start with either one. Your choice.
Describe the theoretical probability
Reasoning
Describe an experimental probability
The data
Summarize the class data.
What did you learn about probability?
What else did you learn?
Fact Sheets
Famous Coin tosses
Around 1900 Karl Pearson tossed a coin 24,000 and recorded 12,012 heads.
John Kerrich, while a prisoner of war, tossed a coin 10,000 times and recorded some of the following results:
| Number of tosses | Number of heads |
|---|---|
| 10 | 4 |
| 50 | 25 |
| 100 | 44 |
| 500 | 255 |
| 1,000 | 502 |
| 5,000 | 2,533 |
| 8,000 | 4,034 |
| 10,000 | 5,067 |
Word bank
- Probability of an outcome is the number of specific outcomes, out of the total number of all possible outcomes for a particular event.
- Event is a thing that happens. Example, a coin flip.
- Events can be predicted as: impossible, possible, likely, unlikely, or certain. What percent can be associated with each?
- Outcome is a specific result of of an event. Example, an outcome of a coin flip is heads or tails.
- Theory is an idea used to explain or predict an event.
- Experiment is a test or set of trials made to try to understand something.
- Probability can be determined in one of two ways: theoretical and experimental.
- Experimental probability is determined by repeating a certain event a number of times and collecting numerous results to determine the probability. Example
- Theoretical probability is determined with reasoning, by generating all the possible outcomes, or combinations, of outcomes in an event. Example
Three coin toss
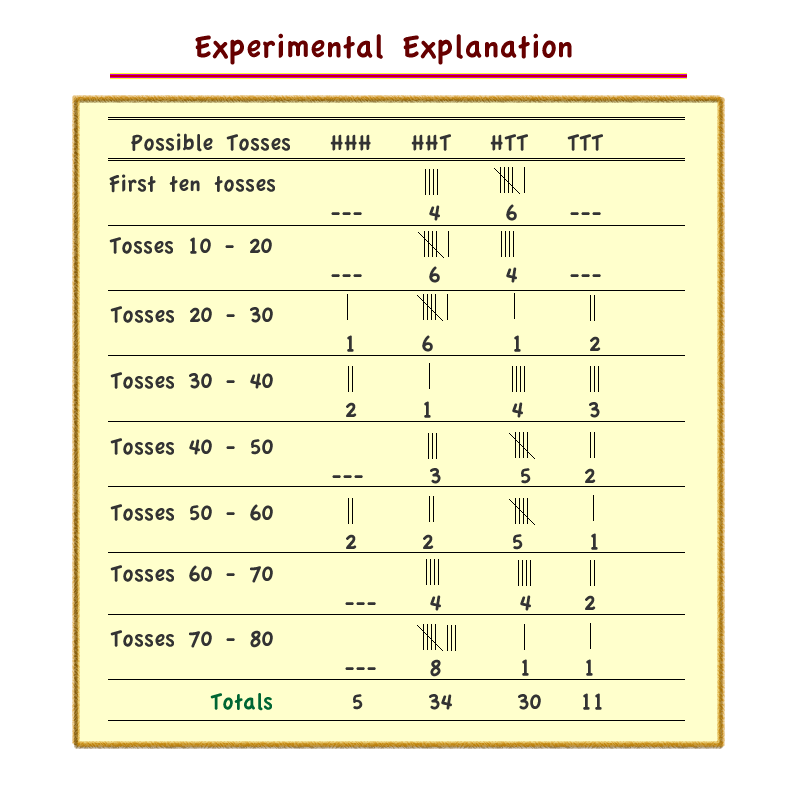
Three coins toss example
Experimental eample for outcomes of a three coin toss.

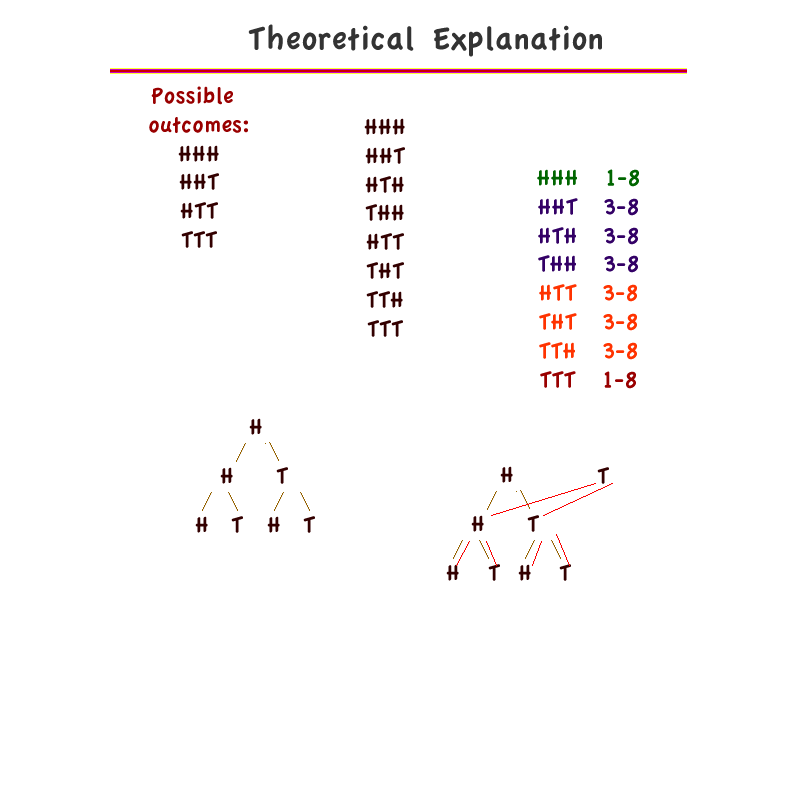
Example of a theoretical explanation of a three coin toss

Home: Pedagogy - theory, curriculum, learning, human development, & teaching
Home: Math - knowledge base, activities, pedagogical knowledge in all 10 dimensions