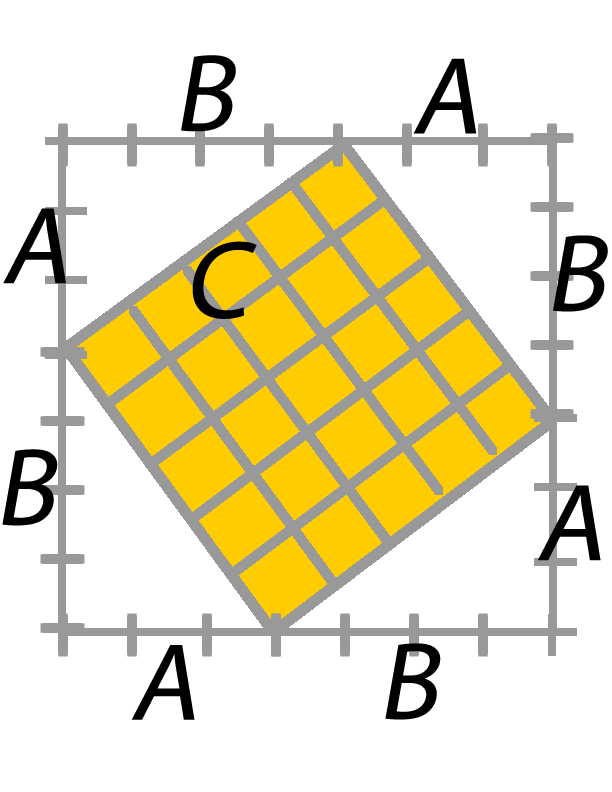
Pythagorean Theorem
Solving for the length of the hypotenuse (C).
A traditional proof for Pythagorean theorem uses the area of the sides to justify the length of
a2 + b2 = c2, while the focus of the equation focuses on the length of the sides of a right triangle.
The key idea to remember, when doing so, is you are trying to verify, or find, the length of C.
Look at the two explanations in the figures below.
The first, uses areas to verify the length of C.
The second, focuses a bit more on lengths to verify the length of C.
Below the examples is a work sheet to verify the second model.

Jumbo Square Inscribed in Four Triangles - work sheet
- The area of Yellow square = 25
- It is a square, therefore all sides are equal length (5).
- Print this sheet.
- Cut along the perimeter of the largest grey square.
- Fold each of the four triangles along their hypotenuse.
- It covers all but one square.
- Why?