Sudoku
An introduction to a puzzle of reasoning and logic
Directions:
Fill in the grid with numbers 1 thru 9
so every column, row, and 3 x 3 square
has the numbers 1 thru 9 only once
in each column, row, and square.
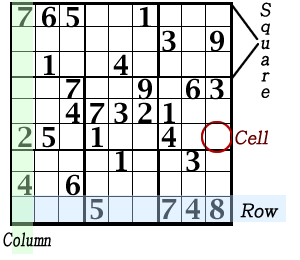
Source Michael Rios (2005). Green Belt SUDOKU. Sterling Pub. Inc., NY, ISBN: 1-4027-3596-0
![]()
Conjectures & Hints from obvious to not obvious:
Obvious
- Each numbers 1-9 is uniquely placed in the nine cells of each square, column, or row.
- If a square is filled with all but one number, then the remaining number, 1-9, goes in the empty cell of that square.
- If a column or row is filled with all but one number, then the remaining number, 1-9, goes in the empty cell.
- Any row or column that intersects each other has the same number at the intersecting cell and only in that cell.
- Cells without numbers can eliminate all numbers in rows and columns that intersect the cell, as possible values for inclusion in the cell.
- Three squares grouped as a horizontal row or a vertically column (cells in a 3x9 rectangle made with adjacent squares) will have one of 1-9 numbers in each of the three different rows or columns for the three square row or column groups.
- Identical numbers in other cells can be used to eliminate open cells in other squares and identify a cell where that number belongs. Example, in sample above. #1 is in the top row and #1 is in the third row. Therefore, consideration of #1 in the top row and bottom row of the top right sqare cn be eliminated. Making the only possible placement of the #1, in the top right square, as in the second row in the open cell between the 3 and 9.
- If there are only two identical possible numbers that could be in two cells of the same column or row that are in the same square, and are not included as possible numbers forother cells in tha row or column, then those numbers will be located in one of those two cells and can be eliminated from placement in other cells in that square.
{ [(5,7)(5,7)(3,6,9)] [(1,2,3)(6)(9] [(4,6)(2,3)(9)]} - XY Wing solution
Not Obvious
Outstanding sources
Solution for Sample puzzle
